Nnye módszerek a probléma megoldására (3
Mi magyarázza az alapvető fogalmak használatával kapcsolatos numerikus módszerek.
Bemutatjuk a t változó egyenletes rács lépése h> 0. azaz úgy a pontok halmaza.
1. Euler módszer. Egyenlet (3.1) helyébe a differencia egyenlet
.
A megoldás ennek az egyenletnek egyértelműen a kiújulás képlet.
Hiba módszer. Ha

A 6. fejezetben vizsgáltuk:
Cauchy probléma elsőrendű differenciálegyenlet.
Módszerek a numerikus megoldása elsőrendű differenciálegyenlet.
Euler módszer és hiba.
Runge-Kutta másodrendű pontosság és hiba.
Runge-Kutta módszer harmadik rendje pontosság és hiba.
Runge-Kutta módszer negyedrendű pontosság és hiba.
2. Az eljárás Runge - Kutta másodrendű pontosságát.
Tegyük fel, hogy egy közelítő értéke



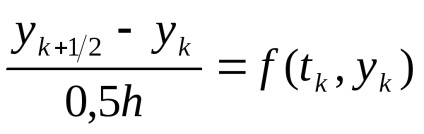
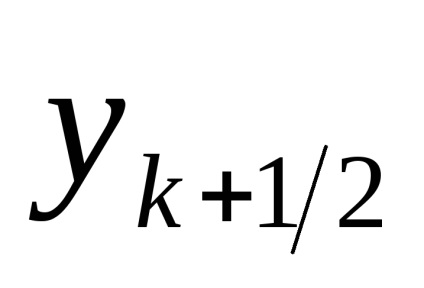

Hiba módszer. Ha

3. Az eljárás Runge - Kutta harmadrendű pontossággal.
Hisszük, hogy a probléma megoldása (3.1) - (3.2), a lényeg

, ahol

4. Runge - Kutta negyedrendű pontossággal.

, ahol

Megjegyzés. Runge-Kutta módszer is alkalmazható, ha az ismeretlen függvény egy vektor, azaz
Az előadás 7 megtudtuk:
Runge-Kutta másodrendű pontosság és hiba.
Runge-Kutta módszer harmadik rendje pontosság és hiba.
Runge-Kutta módszer negyedrendű pontosság és hiba.
Véges-különbség közelítése az első derivált és annak pontosságát.
Véges-különbség közelítése a második derivált és annak pontosságát.
A véges differencia közelítése az első derivált és a második származékot kapjuk a meghatározása. A terjeszkedés a funkciók a szomszédságában lévő X Taylor sorba fennmaradó részt Peano formáját, megkapjuk a jobb és a bal véges különbségek, valamint közelítő második derivált.
Az előadás 8 tudtuk, hogy közelítse első és második származékai a funkciót.
A probléma a hőátadás az olaj szállítása gázvezeték.
A matematikai modell hőátadás problémák az olaj szállítása gázvezeték.
4. § A probléma a hőátadás az olaj szállítása gázvezeték. A differenciálegyenlet másodrendű. határ érték probléma
1. fajta.
4.1. Nyilatkozat a problémát.
Feladat 4. Hosszú vezetéket a hővezetési λ (kcal / m.chas C.) A termikus egyensúlyban, azaz csövek pontok nem változik a hőmérséklet az idő. Keresztüli hőveszteség a cső felületén a környezetben, amelynek hőmérséklete θ0 = const. arányos a hőmérséklet-különbség konstans hőátadási együtthatója α (kcal / m2 óra C.). Feltételezve, θ hőmérséklet minden tochah keresztmetszete a cső állandó, megtalálja a függőség θ = θ (x) a koordináta, mért bármely végén.