Négyszög - Kelj fel! At Antoshka
Definíció 1. téglalap - sík geometriai alakzat, amely négy pontot, kötve sorokat úgy, hogy nincs közös pontjuk kivételével bárhol ezekben nagyon pontokat.
Definíció 2. Téglalap - egy téglalap, amelynek két szemben lévő oldala egyenlő és mind a négy sarka egyforma.
Négyszög egy paralelogramma, négyzet vagy rombusz. Ezért lehetséges megfogalmazni a meghatározása a téglalap.
Definíció 3. téglalap - paralelogramma, amely mind a négy sarka egyenes.
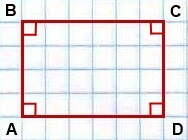
A hosszú oldalon a téglalap hívják a hossza a téglalap, és rövid - szélessége a téglalap.
Mindkét fél a téglalap magassága.
A főbb jellemzői a téglalap
1. A két ellentétes oldalán a téglalap azonos hosszúságú, azaz, ezek a következők:
2. A másik oldalon a téglalap párhuzamos:
3. A szomszédos oldala a téglalap mindig merőleges:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Mind a négy sarkából a téglalap sorokat:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90 °
5. A sarkokban a téglalap egyenlő az összege 360 fok:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360 °
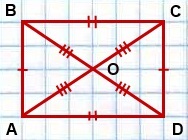
7. A négyzetösszege az átlós a téglalap egyenlő a négyzetösszeg oldalainak:
2 2d = 2a + 2b 2 2
8. Minden egyes téglalap átlós osztja a téglalap két egyenlő részre, nevezetesen, a derékszögű háromszög.
9. téglalap átlóinak metszéspontja a metszéspont oszlik ketté:
AO = BO = CO = DO = d / 2
10. Az metszéspontja az átlók a téglalap hívják központ és a központ a körülírt
11. A méret a téglalap az átmérője a körülírt kör
A hossza a téglalap hívják a hossza a hosszabb pár oldalon.
A szélessége a téglalap nevezzük hossza rövidebb pár saját oldalán.
Gyakran problémát szükség ahhoz, hogy a hossza a téglalap alatt biztosítja képletek erre
Formula meghatározására oldalak hosszát a téglalap
1. Képlet a téglalap (hossza és szélessége a téglalap) keresztül egy átlós, és a másik oldalon:
a = √ (d 2 - b 2) és a, illetve b = √ (d 2 - a 2)
Bizonyítás: Tulajdonság 2 7. 2d = 2a + 2b 2 2 # 8658 (Time részleteket lerövidíti 2) d 2 = a 2 + b 2 # 8658 egy 2 = d 2 - b 2 # 8658 a = √ (d 2 - b 2)
2. A képlet a téglalap (téglalap hosszúság és szélesség) az egész tér, és a másik oldalon:
a = S / b, illetve és b = S / A
Bizonyítás: S = a • b # 8658 a = S / b vagy b = S / A
3. A képlet a téglalap (hossza és szélessége a téglalap) és ezen keresztül a kerülete a másik oldalon:
a = (P - 2b) / 2, illetve és b = (P - 2a) / 2
Bizonyítás: P = 2 (a + b) # 2 8658 b = (P - 2a) # 8658 b = (P - 2a) / 2
4. A képlet a téglalap (téglalap hossza és szélessége) az átmérő és az a szög α:
a = d sinα és ennek megfelelően b = d cosa
5. A képlet a téglalap (téglalap hossza és szélessége) az átmérő és az a szög β:
a = d sin β / 2 és rendre, b = d cos p / 2
Átlós egy téglalap bármilyen szegmens összekötő két csúcsai a szemközti sarkait egy téglalap.
Formula hosszának meghatározására átlójának egy téglalap
1. Formula téglalap átlósan két oldalán a téglalap (a Pitagorasz-tétel):
Bizonyítás: A négyzetének összege a diagonális a téglalap egyenlő a négyzetösszeg oldalainak:
2 2d = 2a + 2b 2 2
2. A képlet a téglalap átlósan a téren, és akár úgy:
d = (√ (S 2 + 4)) / a = (√ (S 2 4 + b)) / b
3. Formula téglalap átlósan a kerülete, és bármely irányba:
d = (√ (P 2 - 4 Pa + 8a 2)) / 2 = (√ (P 2 - 4PB + 8b 2)) / 2
4. Formula téglalap átlósan a sugara a körülírt kör:
5. Formula átlósan keresztül a téglalap körülírt kör átmérője:
6. Formula téglalap átlósan a sine a szög az átlós, és a hossza a szemközti oldalon a szög:
7. Formula téglalap átlósan keresztül koszinusza a szög mellett a átlós hossza az oldalsó és szomszédos a sarokban:
8. Formula átlósan át a téglalapot sine közötti hegyesszög átlói a téglalap és a terület
Kerületének egy téglalap az összege hosszának minden oldalról a téglalap.
Formula hosszának meghatározására a kerülete egy téglalap
1. Az általános képletű kerületének egy téglalap két oldala a téglalap:
P = 2a + 2b, vagy P = 2 (a + b)
Onlyayn számítani a kerülete itt
2. A képlet a kerületének egy téglalap egész területen, és mindkét oldalán:
P = (2S + 2a 2) / a = (2S + 2b 2) / b
3. A képlet kerületének egy téglalap fölött az átlós és mindkét irányban:
P = 2 (a + √ (d 2 - a 2)) = 2 (b + √ (d 2 - b 2))
4. Képlet téglalap alakú kerületet a sugara a körülírt kör és bármely irányba:
P = 2 (a + √ (4R 2 - a 2)) = 2 (b + √ (4R 2 - b 2))
5. Képlet téglalap kerületét az átmérője a körülírt kör és bármely irányba:
P = 2 (a + √ (Do 2 - a 2)) = 2 (b + √ (Do 2 - b 2))
Területe a téglalap határolt térben oldalán téglalap, azaz kerületén belül a téglalap.
Képletek területének meghatározására egy téglalap
1. Formula téglalap területe két szempontból:
Online területének kiszámítására egy téglalap itt lehet
2. képlet a téglalap területe a kerülete, és bármely irányba:
S = (Pa - 2a 2) / 2 = (Pb - 2b 2) / 2
3. Formula téglalap területe keresztül átlós és mindkét irányban:
S = a√ (d 2 - a 2) = b√ (d 2 - b 2)
4. Formula téglalap keresztül átlós négyzetes és a sinus közötti hegyesszög átlók:
5. Képlet a téglalap területe által leírt kör sugara és bármely irányba:
S = a√ (4R 2 - a 2) = b√ (4R 2 - b 2)
6. Képlet a téglalap területe az átmérője a körülírt kör és bármely irányba:
S = a√ (Do 2 - a 2) = b√ (Do 2 - b 2)
Leírt kört a téglalap köré
Leírt kört a téglalap köré hívják kör átmegy a négy csúcsa egy téglalapot, amelynek középpontja metszéspontjában az átlók a téglalap.
Képletek meghatározására sugarú körben körülvevő téglalap
1. Formula sugara köré írható kör téglalap két oldala:
2. Formula sugara köré írható kör téglalap és ezen keresztül a kerülete egy négyzet bármely irányba:
R = (√ (P 2 - 4 Pa + 8a 2)) / 4 = (√ (P 2 - 4PB + 8b 2)) / 4
3. Formula-es sugarú körben körülvevő téglalap keresztül tér közelében
R = (√9S 2 + 4)) / 2a = (√ (S 2 + b 4)) / 2b
4. Formula sugara köré írható kör téglalap keresztül négyzet átlójának:
5. Formula sugara köré írható kör téglalapot az átmérője a körülírt kör:
6. Formula sugarú kör körül a téglalap által leírt sine a szög az átlós és a hossza a szemközti oldalon ez a szög:
7. Formula sugara köré írható kör téglalap a koszinusz a szög mellett a átlós hossza az oldalsó és szomszédos a sarokban:
8. Formula sugara köré írható kör téglalap szinuszból között hegyesszöget átlói a téglalap és a terület:
Az oldalai közötti szög és átlók a téglalap
Formula meghatározza a oldalai közötti szög és átlók
1. Az általános képletű meghatározó oldalai közötti szög és átlók a téglalap keresztül átlós és oldalsó:
sin α = a / d, illetve és a cos α = b / d
2. A képlet meghatározó oldalai közötti szög és átlók a téglalap által bezárt szög átlók:
A bezárt szög átlói a téglalap
Formula meghatározza a szöget közötti átlói a téglalap
1. Az általános képletű meghatározó közötti szög átlói a téglalap által oldalai közötti szög és átlók:
2. A képlet meghatározó közötti szög átlói a téglalap átlós át a téren, és: