Négy képletek lehet számítani a területen a rombusz

Rhombus - egy speciális alakja geometria. Sajátos jellemzői, van nem egy, hanem több képletek, amellyel a terület számított rombusz. Milyen tulajdonságai és mik a leggyakoribb formula találni a terület ez a szám van? Nézzünk szembe a tényekkel.

Milyen geometriai alakzat nevezett rombusz

Mielőtt megtudja, mi az a terület, a rombusz, tudnia kell, hogy milyen szám.

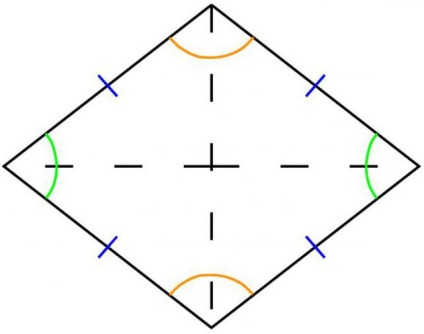
Mivel a rombusz euklideszi geometria nevezzük szimmetrikus négyszög, amelynek négy oldala egyenlő egymással a hossza mentén és egymással párhuzamos.

A kifejezés eredetét

A cím ez a szám jön a legtöbb modern nyelvek a görög, latin, közvetítés útján. „Őse” a „gyémánt” volt a görög főnév ῥόμβος (tambura). Bár a lakosok a huszadik század használt kerek tambura, nehéz elképzelni, hogy a különböző formákat, de a görögök, ezek hangszerek hagyományosan készült nem kerek, és rombusz alakú.

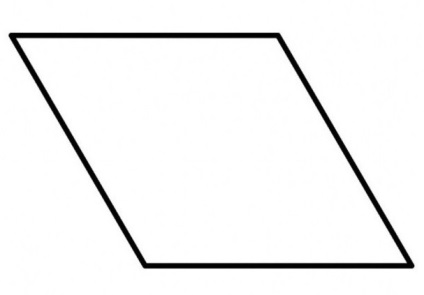
A legtöbb modern nyelvek aktív matematikai kifejezést használnak, mint a latin: rombus. Azonban az angol néha gyémánt gyémánt (rombusz vagy gyémánt). A becenevet, ez a szám volt köszönhető, hogy a különleges formájú, emlékeztet egy ékszer. Általában az ilyen kifejezést használnak nem minden rombuszok, és csak azokat, amelyek szöge metszéspontja a két oldalának egyenlő negyvenöt vagy hatvan fok.

Ez az első alkalom ez a szám már említettük írásaiban a görög matematikus, aki élt az első században - Hérón.

Milyen tulajdonságokkal rendelkezik ez a geometriai alakzat

Találni egy rombusz alakú terület, mindenekelőtt tudnunk kell, hogy milyen funkciók adott geometriai alakzat.

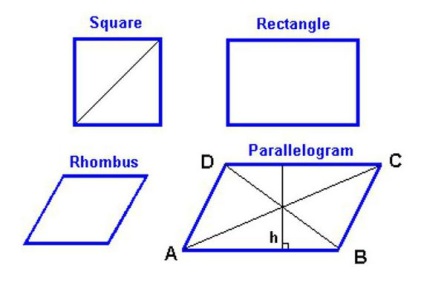
Mint már említettük, a definíciója egy rombusz, ez egy négyszög. És az az oka, hogy a két ellentétes oldalán páronként párhuzamosak egymással, a gyémánt is nevezik paralelogramma, ami azt jelenti, hogy figyelemmel a legtöbb tulajdonságait figury.Obe átlói rombusz annak kereszteződés egyenletesen oszlik ketté. És annak a ténynek köszönhető, hogy azok metszik szögben kilencven fokkal, osztva átlósan 4 háromszöget kitalálni pryamougolnyh.V bármely rombusz átlói osszuk két sarkok, hogy mind a bissektrisami.Esli mindkét átlói rombusz hatványát a tér, a az összeg egyenlő lesz a termék a tér oldalán a figura és a sorok száma csatlakozni chetyre.Esli közepén a négy oldalán a rombusz, a kapott szám lenne pryamougolnikom.Esli gyémánt (függetlenül annak sarkai) a beírt kör, majd saját középpontja mérkőzések diagonaley.Diagonali keresztezi középtengelyei gyémánt kapcsolatba vele szögben kilencven szimmetria gradusov.Poskolku minden oldalán egy rombusz egymással azonosak hossza mentén kerülete képlettel számítjuk ki P = 4 x K (K - a hossza az egyik oldalon).

Milyen feltételek mellett paralelogramma rombusz

Amint az ismeretes, minden rombusz paralelogramma, de nem csak a paralelogramma - egy gyémánt. Ahhoz, hogy pontosan azt állítják, hogy ez a szám mutatja valóban egy gyémánt, és nem csak egy paralelogramma, meg kell felelnie a három főbb jellemzői, amelyek megkülönböztetik a gyémánt. Vagy mindhárom egyszerre.

A átlók a paralelogramma metszik szögben kilencven gradusov.Diagonali szét két szög, meghatalmazotti csak párhuzamosan, de szomszédos oldala azonos hosszúságú, mint a bissektris.Ne. Ezen a módon, az egyik fő különbség a rombusz és paralelogramma, hiszen a második szám az azonos hosszúságú csak párhuzamos oldalú, de nem szomszédos.

Milyen feltételek mellett egy négyzet alakú gyémánt

Szerint a tulajdonságok bizonyos esetekben a gyémánt egyszerre válhat egy négyzet. Ahhoz, hogy vizuálisan is megerősíteni ezt az állítást, egyszerűen forgassa a tér bármely irányba negyvenöt fokos. Az eredményül kapott szám lenne egy rombusz, mindegyik sarkában, amely egyenlő kilencven fokkal.

Továbbá, annak igazolására, hogy a tér egy rombusz, össze lehet hasonlítani jellemzői ezek a számok: mindkét esetben minden oldalról egyenlő, és az átlók a szögfelezői és metszik szögben kilencven fokkal.

Hogyan lehet megtalálni a területet a rombusz segítségével átlók

A mai világban, az interneten is megtalálható szinte az összes anyagát elvégzi a szükséges számításokat. Tehát bőven van erőforrás, felszerelt szoftver automatikusan kiszámítja a területet egy adott alakú. És ha (mint ahogy az a rombusz alakú) számos képletek erre lehetőség van, hogy melyik közülük kerül ki a legkényelmesebb. De mindenek felett, akkor képesnek kell lennie arra, hogy az maximálisan Rhombus terület a számítógép használata nélkül, és keresse a képleteket. Számukra van egy rombusz alakú sokat, de a leghíresebb ezek négy.

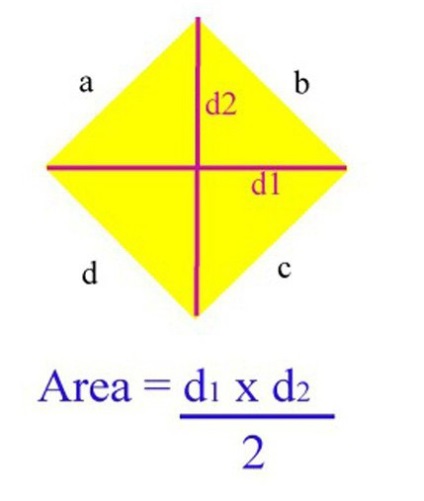
Az egyik legegyszerűbb és leggyakoribb módja, hogy megtalálják a terület ez a szám, ha van információ a hossza az átlók. Ha a probléma az adatok, ilyen esetben tudjuk alkalmazni a következő képlet, hogy megtalálják a nagysága: S = KM x LN / 2 (KM és LN - diagonálisan KLMN rombusz).

Akkor érvényességének ellenőrzésére ez a képlet a gyakorlatban. Tegyük fel, KLMN rombuszt hossza egyik átlós CM - 10 cm-es, és egy második LN - 8 cm-es Ezután helyettesítse az adatokat a fenti képlet, és megkapjuk a következő eredményt :. S = 10 x 8/2 = 40 cm2.

A képlet a terület a paralelogramma

Van egy másik képlet. Mint már említettük, a definíciója egy rombusz, ez nem csak egy négyszög, hanem egy paralelogramma, és mindazokat a funkciókat ez a szám. Ilyen esetben, hogy megtalálja a területen igen megfelelő használata a képletet kell alkalmazni a paralelogramma: S = KL x Z. Ebben az esetben a KL - hosszú oldalai a paralelogramma (rombusz), és Z - egy hosszú magasság húzott erre az oldalra.

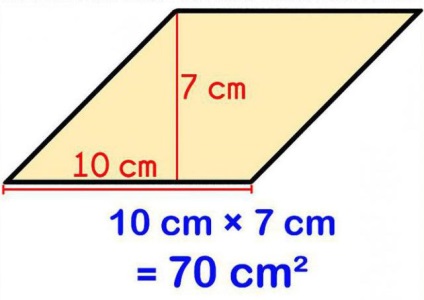
Az egyes feladatok nem kapnak a hossza az oldalon, de ez ismert a kerülete egy rombusz. Mivel a helyszín fenti képlet lett megadva, ez segíthet felfedezni hosszú oldalon. Így, a kerülete a ábra -. 10 cm hosszú oldalán megtalálható megfordításával a kerülete a 10 képletű, és elosztjuk 4. Az eredmény az lesz, 2,5 cm - ez a kívánt hosszúságú oldalán a gyémánt.

Most meg kell próbálni helyettesíteni ezt a számot a képlet, tudva, hogy a hossza a magasságot húzott az oldalon is egyenlő 2,5 cm. Most nézzük meg, hogy ezeket az értékeket a fenti képlet a terület egy paralelogramma. Kiderült, hogy a rombusz terület S = 2,5 x 2,5 = 6,25 cm 2.

Egyéb számítási módszerek rombusz területe

Azok, akik már elsajátították a szinusz és koszinusz lehet használni, hogy megtalálják a terület egy rombusz tartalmazó képletek azokat. A klasszikus példa a képlete a következő: S = KM2 x Sin KLM. Ebben az esetben a terület a szám a termék két oldalán egy rombusz, szorozva a szinusz a szög közöttük. És mint minden szempontból azonos gyémánt, akkor könnyebb csak azért, hogy az egyik oldalon a tér, ahogy az a képlet.

Ellenőrizze a gyakorlatban ez a rendszer, nem csak a gyémánt, és a tér, amelyről ismert, hogy a sarkok egyenesek, és ezért ezek kilencven fokkal. Tegyük fel, hogy az egyik oldalán egyenlő 15 cm. Az is ismert, hogy a szinusz a szög 90 ° egyenlő egységét. Ezután, az alábbi képlet szerint, S = 15 x 15 x 90 ° = Sin 255h1 = 255 cm2.

Amellett, hogy a fenti, egyes esetekben, a másik képlet használható, a szinusz területének meghatározására a rombusz: S = 4 x R2 / Sin KLM. Ebben a kiviteli alakban, egy sugara beírható kör a gyémánt. Felemelkedik, hogy a hatalom a tér, és néggyel szorzott. És az eredmény osztva a sine a szög, közel a beírt szám.

Példaként az egyszerűség kedvéért a számítások figyelembe ismét négyzetes (sine irányszögével lesz mindig egyenlő egység). . A sugara a beírt kör - 4.4cm Akkor rombusz terület kerül kiszámítani: S = 4 x 4,42 / Sin 90 ° = 77,44 cm2

A fenti képletek megtalálják a sugara rombusz - nem az egyetlen a maga nemében, de ezek a legtöbb könnyen érthető és számítások elvégzésére.

Kievyan utca 16 0016 Örményország, Jereván 374 11233255