Mintaoldatokat Taskbook Kuznyecova l
Nyilatkozat a problémát. A differenciálegyenlet
módszer isoclines konstrukció szerves görbét ponton áthaladó.
Tétel (Cauchy). Ha a függvény folytonos a ponton, és a közelében, van egy megoldás a (2) egyenlet, oly módon, hogy. Ha a parciális függvény deriváltját is folyamatos, akkor ez a megoldás egyedülálló.
A Cauchy probléma egy elsőrendű differenciálegyenlet összetétele a következő. A megoldás keresése (integrál) a differenciálegyenlet (1) vagy (2), amely megfelel a kezdeti feltétel (). Geometriai szempontból ez azt jelenti, hogy többek között a szerves görbék az egyenlet kell találni azt, amelyik átmegy egy adott ponton.
A geometriai értelmezése a differenciálegyenlet (2) áll, az a tény, hogy minden ponton a régióhoz tartozó, amelyben az összes körülmények között Cauchy-tétel, beállítja az irányt a húzott érintő egyetlen integrál egyenlet (2) ponton áthaladó, vagyis, mező irányok terén.
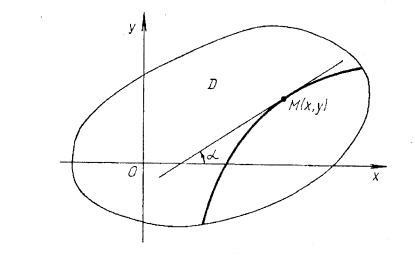
A (2) egyenlet izolálhatjuk egyparaméteres családja görbék, amelyek mindegyike úgynevezett izoklin. Amint meghatározásából következik, valamint az egyes izoklina területén irányban folyamatosan, azaz .
Megtalálása isoclines és irányokat, amelyek mentén lehetővé teszi, hogy megszervezze a területén irányok és körülbelül megépíteni a szerves görbék a differenciálegyenlet, azaz grafikusan integrálni ezt az egyenletet.
8. feladat Egy adott differenciálegyenlet módszerrel isoclines konstrukció szerves görbét ponton áthaladó.
.
Írunk az egyenlet a következő formában:
.
Mi konstrukció az irányt mezőt a differenciálegyenlet. Isoclines megfelelő mező területek meredeksége egyenlő a, vagy, azaz egyenes.
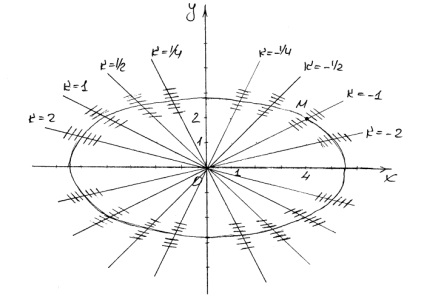
A szerves görbe nyilvánvalóan elliptikus alakúak.