Mérése áramlási sebesség és a folyadék áramlási
Tekintsük az alkalmazás a Bernoulli-egyenlet az áramlási sebesség mérésének egyszerű eszközök, mint például a Pitot-csővel - Prandtl Venturi.
Ahhoz, hogy meghatározzuk a sebességét egy szabad áramlás (például egy csatorna) használja a Pitot-csővel, amely meg van hajlítva derékszögben egy kis átmérőjű csövet, hogy van telepítve az áramlás felé nyitott alsó vége a mozgása a folyadék (ábra. 3.9).

A repülőgép-összehasonlítás 0-0 gondoskodjon egy vízszintes tengely mentén a cső. Úgy döntünk szakasz 1-1 bizonyos távolságra a csövet, és a szakasz 2-2 a bevezető cső. A geometriai magassága a súlypont a keresztmetszetek Z1 és Z2 jelentése nullával egyenlő. A súlypont a szakasz 1 - 1 folyadék rendelkezik mozgási energia és a potenciális miatt a folyadék oszlop magassága h1. ahol p - a hidrosztatikai nyomás.
Ha folyékony részecskék azok csőben sebessége válik nullával egyenlő, a kinetikus energia átalakul potenciális, és a folyadék a csőben fölé emelkedik, a szabad felülete a h2 magassága. egyenlő sebességű fejét. A tömegközéppont a keresztmetszet 2 - 2 folyadéknak potenciális energiája a folyadékoszlop magassága h1. és a potenciális energia, mozgási egyenlő. Mi alkotják a Bernoulli-egyenlet kivételével hpot nyomásesés:
Ez az arány a folyadék mozgását. Valójában ez valamivel alacsonyabb sebességet, mivel a számításokat végeztünk figyelembevétele nélkül nyomásveszteséget. Határozza meg a tényleges áramlási veszteség tényező figyelembe veszi a sebesség sebesség # 966;. amelyet kísérleti úton határozzuk meg. Az arány:
ahol h - a magassága a folyadékoszlop a csőben fenti szabad felszíni szinten.
A nyomás a csövet a szabad felület szintje létre rovására a kinetikus energia a folyadékáramlás:
ahol pg - a hidrodinamikus nyomás.
folyadéknyomás által generált sebesség fej, az úgynevezett hidrodinamikus nyomás.
Ahhoz, hogy meghatározzuk az áramlási sebesség a nyomás Pitot-csővel a kérelmet, - Prandtl szám, amely kombinálva van egy eszköz és egy hagyományos pitotcsővel pezometr (3.10. Ábra). A magasság a folyadékoszlop képződik a Pitot-csővel miatt hidrosztatikus és hidrodinamikus nyomás pezometre - csak hidrosztatikus.

Ábra. 3.10. Pitot - Prandtl
A különbség a folyadék szintje a csövekben # 8710; H értékét adja meg a sebesség fej. és ahol az áramlási sebesség határozza meg, figyelembe véve a sebesség korrekciós tényező # 966; :
Venturi áramlásmérő olyan simán konvergens és divergens hengeres betételem telepítve a csőben (ábra. 3.11). A kiterjesztett és szűkült részei a mérő telepített pezometry.

Ábra. 3.11. Venturi
Mi alkotják a Bernoulli-egyenlet relatív összehasonlítás sík egybeesik a tengelye az áramlásmérő. Szekcionált helyszíneket választanak pezometrov kapcsolatokat. Mivel a tömegközéppont a keresztmetszetek síkjában az összehasonlítás, geometriai magassága Z1 és Z2 jelentése nullával egyenlő.
Egy ideális folyadék kivételével nyomásveszteség hpot Bernoulli egyenlet:
A kontinuitási egyenlet áramlási:
Behelyettesítve az értéke V2 sebesség egyenlet (3.11) egyenletbe (3.12):
Mivel a sebesség V1 - ideális áramlási sebessége, az áramlási sebesség, meghatározni ezt a sebességet, elméletileg:
ahol a C - elméleti állandó áramlásmérő.
A tényleges áramlási sebesség:
ahol C - igazi állandó áramlásmérő;
k - az együttható, amely figyelembe veszi a nyomásveszteséget, mikor a folyadék átfolyik egy áramlásmérő, empirikusan határozzuk meg.
folyadékáramlás rezsimek
Két mód a folyadék áramlását - lamináris és turbulens.
A mozgást, ahol nincs változás (feszültségingadozás) a helyi sebességvektor az úgynevezett lamináris áramlás (a latin szó «lamina» - réteg). A folyadék minősül több különálló rétegek, különböző sebességgel mozgó, keverés nélkül egymással. Mozgása a folyadékot, amelyben van egy változás (hullámosság) a lokális sebesség vektor, ami a keverési folyadék, úgynevezett turbulens (a latin szó «turbulentus» - rendezetlen, kaotikus).
Modellezése folyadékáramlást egy kör alakú cső tartott O. Reynolds 1883-ban egy növény ábrán látható. 3.12. Elején üvegcső van elhelyezve egy vékony cső színű folyadék, amelyeknek a sűrűsége egyenértékű volt a sűrűsége a fő folyadék áramlását. A kis áramlási sebességű áramát színezett folyadék mozog, lényegében egyenes vonalú és vízszintesen, ami azt bizonyítja, a laminátum (lamináris) áramlását a folyadék (ábra. 3,12, a).
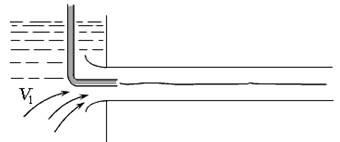

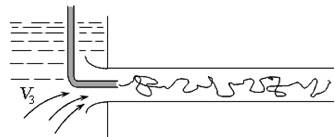
Ábra. 3.12. folyadékáramlás rezsimek:
a) - lamináris; b) - átmenet; c) - a turbulens
A növekedést a fő áramlási csepegtető áramlás lelassul, hullámos jellegét, eltöri fordulnak elő, ami jellemző a labilis, tranziens (ábra. 3,12, b). A további növekedés a áramlási sebesség színezett csepegtető teljesen elegyedik a folyadékkal, ami azt bizonyítja, rendezetlen (turbulens) áramlás (ábra. 3.12).
Jellemzésére folyadékáramlás elfogadott rendszert dimenziómentes kritérium - Reynolds szám: Re. A kerek csövek átmérője d:
ahol # 957; - kinematikai viszkozitási együtthatót.
A kísérletek alapján a kerek csövek a kisülési áram a kritikus Reynolds-számnak, amely turbulens válik lamináris, valamint Re = 2300. A folyadék áramlási sebessége megfelel a változás az áramlási rendszer, az úgynevezett kritikus sebesség.
Gyakorlati számítások feltételezhető:
- Re <2300 существует ламинарный режим течения;
- ha Re> 2300 van egy turbulens áramlású.
Ehelyett átmérőjű Reynolds szám például az olyan lineáris paraméter jellemző az élő részt. A nem-kerek csövek vagy szabad áramlását, a szabad felület képező jellemző lineáris mérete határozza meg a hidraulikus sugár R. arány (3.1):
A kritikus Reynolds-szám kerül rögzítésre a hidraulikus sugár, egyenlő Re ≈ 580.

Ábra. 3.13. Görbén a réteges rendszer
A lamináris áramlás diagramja a lokális sebesség az élő szakasz formájában van a parabola (ábra. 3.13), az átlagos áramlási sebesség V kétszer kisebb, mint a maximális (). Együttható Coriolis lamináris folyadék mozgás # 945; = 2.
A turbulens rezsim mozgás jellemzi folyamatos keverés a folyadék részecskék. részecskesebesség bármely ponton az adatfolyamban folyamatosan és állandóan változó időben, azaz impulzus nagyságát és irányát tekintve az átlagos értéket. Mert turbulens áramlás jellemzi olyan kifejezések, mint a pillanatnyi sebesség és átlagoló.
Pillanatnyi sebesség u - a sebessége a folyadék részecskék egy adott pontban egy adott idő alatt. Mivel a pillanatnyi sebesség véletlenszerű időben, akkor bővült egy háromdimenziós koordinátarendszerben a hosszanti UX. keresztirányú uy és uz (). A pillanatnyi változás nagyságát és irányát a részecskesebesség hívják lüktetés.
Átlagoló sebesség - az átlagos részecske sebessége az idővel egy adott ponton, kapott kellően hosszú ideig.
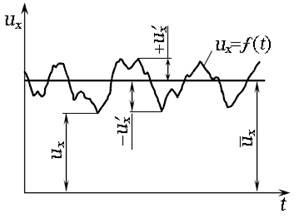
Ábra. 3.14. Graph lüktetés helyi pillanatnyi sebesség:
- pillanatnyi sebesség; - átlagoló a sebességet;
Tekintsünk egy idődiagram, amely a pillanatnyi hosszirányú sebesség ux (ábra. 3.14). Átlagoló mérete (idő) sebesség bármikor a pillanatnyi sebesség megegyezik a pulzusszám, figyelembe véve:
In vivo keresztmetszet turbulens áramlási módban megkülönböztetni mag. ahol a lokális sebesség enyhén változhat, mivel átlagolás, és a viszkózus alréteg vastagsága adatfolyam # 948; (Delta) (ábra. 3.15). Az átlagos áramlási sebesség. Coriolis együttható # 945; = 1.
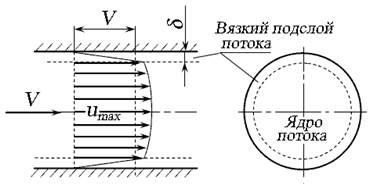
Ábra. 3.15. Reakcióvázlat folyadékáramlást a turbulens áramlás
A viszkózus alréteg patak is nevezik lamináris felületről. érdessége magasság aránya a belső falak a vezeték és a lamináris alréteg áramláskorlátozó felületi folyadék egyaránt jellemzi hidraulikusan sima, durva vagy hidraulikusan. Érdességi magasság falak veszi az átlagos magassága # 8710; Sze
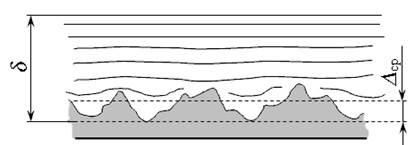
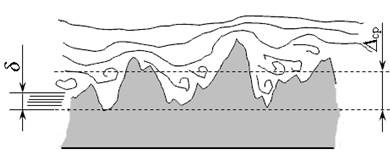
Ábra. 3.16. A felületi érdesség a turbulens:
a) - hidraulikusan sima; b) - hidraulikusan durva
Ha a vastagsága a lamináris alréteg lényegesen nagyobb, mint az átlagos magassága érdesség (# 948;> # 8710; vö), akkor egy ilyen felületen az úgynevezett hidraulikus sima (ábra 3.16, a) .. Ebben az esetben, a felületi érdesség nem befolyásolja az ellenállást a folyadék mozgását.
Ha a vastagsága a lamináris alréteg kisebb, mint az átlagos érdesség (# 948; <∆ср ), то такую поверхность называют гидравлически шероховатой (рис. 3.16, б ). В этом случае при обтекании выступов шероховатости усиливается турбулизация потока, что приводит к увеличению сопротивления движения жидкости и потерь напора.