Megoldás a lineáris egyenletrendszer MS Excel - studopediya
Rövid elmélet során algebra:
Adott egy lineáris egyenletrendszer (1). Mátrix módszer megoldására rendszerek lineáris egyenletek olyan esetekben használjuk, ahol a számos egyenletek száma megegyezik az változó.
Bemutatjuk a jelölést. Legyen A - mátrix együtthatók a változók, B - a vektor abszolút értékben, X - vektor változók. Ezután X = A -1 × B. ahol A -1 - inverz mátrix A. Továbbá, a fordított mátrix A -1 áll fenn, ha a meghatározója a mátrix nem egyenlő 0-val A terméket az eredeti mátrix és az inverz A -1 egyenlőnek kell lennie az identitás mátrix:
Feladat: Oldjuk meg a lineáris egyenletrendszer:
Most lehet, hogy egy érvényesítési talált megoldások x1. x2 és x3. Ehhez hajtsa végre a számítást minden egyes egyenlet segítségével a kapott értékeket x1. x2 és x3. Például a G11 sejtszám értékét. ahol az eredmény meg kell egyeznie a 3. Bemutatjuk a következő képlet = A11 * $ F $ 18 + B11 * $ F $ 19 + C11 * $ F $ 20. Másolja ezt a képletet a két sejt alábbiakban, azaz a A G12 és G13. Ismét kapsz oszlopon szabad feltételeket. Így a megoldás a lineáris egyenletrendszer igaz (ris.80).
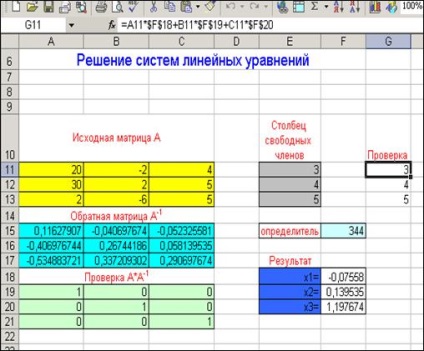
80. ábra - megoldása egy lineáris egyenletrendszer
Lehetőségek az egyes feladatok
Számának beállítása 1. révén a Microsoft Excel kiszámítja a kifejezés értéke:
16. táblázat - Az egyes lehetséges laboratóriumi munka
1. Mi a Függvénytündér?
2. Első lépések a Függvénytündér?
3. Hogyan válasszuk ki a kívánt funkciót?
5. Határozza meg a paraméterek a funkciót?
6. Hogyan kapcsoljuk képletek megjelenítési mód?
7. Melyek a leggyakoribb hibák képletek?
8. Hogyan, hogy megkönnyítse a keresést kapcsolatokat képlet cellákat, amelyekre a formula tartalmaz utalásokat?
9. Mi a neve egy tömb? Array képlet?
10. Milyen módszereket lehet használni a számítások, ami egy sor az eredmények? Merre van megbízhatóbb?