Megoldani egy másodfokú egyenlet, a probléma a pascal, programozás kezdőknek
Megfogalmazás. Valós számok a. b és c. és a bírság 0. Oldjuk meg a másodfokú egyenlet ax 2 + bx + c = 0, vagy jelenteni, hogy nincs valódi oldatok.
Határozat. Algebrai tudjuk, hogy:
Tér uravnenieax 2 + bx + c = 0, vyrazhenieD = b 2 - 4 AC - diszkrimináns:
- esliD> 0 két megoldásokat. ;
- esliD = 0 van egy egyedi megoldást;
- esliD <0, не имеет действительных решений.
Ezért kell számítani a diszkrimináns (hírhedt az ő valós változó d típusú ingatlan), és attól függően, hogy értéket kell megszervezni egy ág. Először meg kell vizsgálni, hogy a tényleges egyenletnek megoldások (azért, hogy a feje az x 1 és x 2 típusú ingatlan). Ha igen, és ha a diszkrimináns nem egyenlő nullával, kiszámítjuk mindkét megoldás szerinti formulák, és ha a diszkrimináns nulla, akkor kiszámítunk egy egyedi megoldást. Ha nincs igazi megoldás, mi származik egy szöveges üzenetet róla. Az alap algoritmus illusztrálja az alábbi folyamatábra:
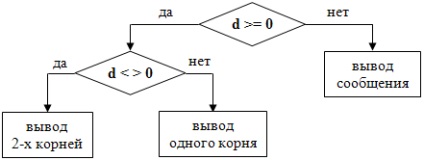
Három megfejtetlen blokk szabványos kimeneti utasítások. Nézzük őket részletesen.
1) A levezetése a két gyök a kifejezés a következő lenne:
x1: = (-B + sqrt (d)) / 2 * a;
x2: = (-B - sqrt (d)) / 2 * a;
writeln ( 'x1 =', X1: 4: 2, 'x2 =', X2: 4: 2);
Ebben az esetben, a megjelenített nézett volna ki, mint ez: „x 1 = m. x 2 = n”. amely kék színnel egyértelmű szöveges állandók, amelyek a felvétel argumentumlistában a writeln. piros - számított értékek x 1 és x 2 Továbbá a gyökerek származnak egy formázott formában az első szám a kettőspont utáni meghatároz egy mező szélessége a kimeneti változó időtartamon (ha a mező szűkössége akkor bontsa a program), és a szám a kettőspont utáni második - a megjelenített karakterek számát frakcionált (nem lehet változtatni működés közben a program);
2) A levezetése ugyanolyan gyökér - mindegy, csak egy gyökér jelenik meg:
3) Mivel a valós gyökereit az üzenet:
writeln ( 'Nincs valódi megoldást!');
Ennek eredményeként a belső feltételes szervezet befogadó fog kinézni:
ha d <> 0, akkor kezdődik
x1: = (-B + sqrt (d)) / 2 * a;
x2: = (-B - sqrt (d)) / 2 * a;
writeln ( 'x1 =', X1: 4: 2, 'x2 =', X2: 4: 2)