Meghatározó a grafikon - studopediya
V. Tekintsük a szett tartalma pont csatlakozik valamilyen módon. Elements - csúcsot. GrafG = G (V) a csúcsok halmaza V egy család kombinációk vagy pár formájában
arról, hogy mely csúcsokat tartják a kapcsolatot.
Összhangban a geometriai ábrázolása a grafikon, minden egyes pár nevezzük egy él (ív) a gráfban, és - végpontot.
Megadhatjuk az elképzelés, hogy a grafikon egyébként, ha elképzeljük ponthalmaz nevű csúcsot V. síkon. és több irányított szegmensek E, összekötő összes vagy néhány, a csúcsok és a nevezett ívek. Ie matematikailag gráf G lehet meghatározni, mint egy pár készletek G = (V, E). Példák a gráf lehet térképet utak vagy vasutak, vegyületet áramkör elektromos áramkörök, stb
Feltételezhetjük, hogy több irányított ív összekötő elemek E. V. több kijelző van beállítva önmagába. Ezért feltételezhetjük, adja meg a gráf, ha adott a csúcsok halmaza V és eljárás megjelenítésére több V T V. Így, a G gráf egy pár (V, T) álló több V T és megjeleníthető megadott ez a készlet.
Például, ábra. 2.1 ábra egy gráf, amelynek csúcsai a pont a, b, c, d, e, g, h, és ívek - a szegmensek (a, a), (c, b), (c, d), (c, e), (d, c), (d, d), (e, d), (g, h). A következő redukált grafikon meghatározása a következő: T a =; T b =Æ; T c =; T d =; T e =; T g =; T h =Æ.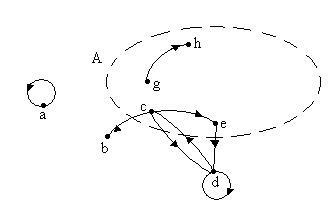
Könnyen belátható, hogy ez a meghatározás a grafikon megegyezik a meghatározása a kapcsolatot a forgatáson.
A fentiek alapján megállapítható, hogy a G gráf (V, E) a készlet két - egy nem-üres halmaz V (csúcsok halmaza) és a beállított E kettős eleme részhalmazát V (E - több bordát).
A definíció az élek lehet venni, vagy nem veszik figyelembe a sorrendben a két végére. Ha ez a sorrend nem lényeges, vagyis if. E jelentése a nem-orientált szélén, és ha a sorrendje fontos, akkor a D nevezzük irányított él, és ahol vi a kezdeti vertex, - végső csúcs.
Egy gráf nevezzük orientált. Ha összpontosítani minden széle.

irányítatlan gráf egy irányított gráf
Egyes esetekben van egy vegyes grafikonok.
Mivel abban az esetben, orientált és nem orientált bordák azt mondják, hogy a széle E = (VI. Vj) van esetet a csúcsok vi és vj, és hogy a csúcsok a VI és vjintsidentny széle E. A két csúcsot incidens úgynevezett szomszédos egyik szélét. Vertex nem esemény bármely szélén az úgynevezett izolált. Gyakran van értelme, hogy csak azokat a nem szigetelt tetején.
Az élek száma esetet a vertex u nevezzük mértékben vertex és nevezzük ° (u).
Graph csak elszigetelt csúcsok, az úgynevezett null grafikon.
A legfontosabb az esetben tele van grafG = (V, E), amelynek élei összes lehetséges pár () két különböző csúcsot vi és vj a V. Egy teljes gráfot csúcsot jelzi. Ábra. 2.3 ábra a teljes beütésszám és volt.
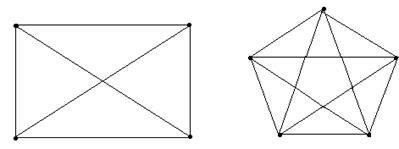
A teljes gráf orientált pár élek, minden irányban egy összekötő bármely két különböző csúcsot vi és vj. A bordák, amelynek mindkét végéről pontok egybeesnek L = (a, a) nevezzük hurok.
(Lásd. Ábra. 2.1 a felső "és", "d"). A hurok általában úgy, hogy nem orientált. Lehet terjeszteni a teljes gráf teljes gráf hurkok, adjunk hozzá egy hurkot minden csúcs.
Feltételezzük, hogy a csúcsai a pár összeköt több különböző bordák.
Minden egyes irányított gráf egy inverz grafG *. a kapott orientációjának megváltozása egyes szélei a G gráf megfordul.
Minden egyes irányított gráf, van még egy járulékos irányítatlan grafGu. élek szélét G. de orientáció nélküli. Néha célszerű átalakítani egy irányítatlan gráf G egy irányított gráf Gd megduplázásával álló eljárással helyettesítése minden borda G pár bordával azonos csúcsok és tulajdonít nekik (éleket) a ellentétes irányítottságban.
Egy gráf úgynevezett lapos, ha nem lehet bizonyítani a síkban úgy, hogy minden él a csúcsai a kereszteződés G.
Rendszeres grafikonok. Graf szabályos vagy egyöntetű, ha minden csúcsot pontosan ugyanazt a fokozatot. Ha a minden csúcsa egyenlő k. akkor a gráf egy reguláris gráf fokú k. Például, egy teljes gráf n-ed rendű rendszeres grafikon fokú k = n-1. Például a rendszeres 3 fokozatú grafikonok úgynevezett kocka vagy 3-értékű grafikonok. Példaként, ábrán. 2.4 egy köbös grafikon Petersen.
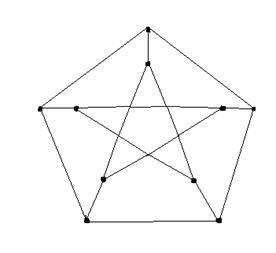
Platóni grafikonok. Platóni gráf egy grafikon által alkotott csúcsok és az élek az öt szabályos poliéder - a platóni testek: tetraéder, kocka, oktaéder, dodekaéder, ikozaéder.
Páros gráfok. Egy gráf úgynevezett páros, ha létezik egy partíciót a csúcsok két osztályba, amelyben a végén minden borda vannak különböző osztályok.
PodgrafomGA gráf G = (V, T) egy olyan grafikon, amely magában foglalja a csak egy részét G csúcsok alkotó halmaz, együtt az íveket, hogy összeköti ezeket a csúcsokat. Például, kontúros szaggatott régió ábrán. 2.1. Matematikailag ez van írva a következő:
Részben gráf GD tekintetében a gráf G = (V, T) egy olyan grafikon, amely csak egy részét az íveket a gráf azaz által meghatározott feltétel
Például, ha a G = (V, T) - térképen Hungary autópályák, akkor a kártya Nizhegorodskaya régió utak jelentése részgráf, és a kártya fő autópályák tartozik - részleges grafikon.
Útján G gráf nevezzük szekvenciáját ívek d = (u1. U2. ... uk), ahol a végén minden előző ív egybeesik az elején a következő. Way d. egymást követő csúcsai csúcsok a, b, c, ... m d jelöli = (a, b, c, ... m).
Putid hossz = (u1. U2. ... uk) az a szám, l (d) = k, egyenlő a ívek száma, melyek az utat d. Néha mindegyik ív ui jóváírásra számos l (ui), az úgynevezett ív hosszát. Ezután az út hossza úgy definiáljuk, mint a hosszának összegét az íveket alkotó pálya
Az, ahogyan a nem ív kétszer fordul elő, az úgynevezett egyszerű. Az, ahogyan a nem vertex kétszer jelenik meg, az úgynevezett elemi.
Áramkör - végső path d = (V1 V2 ... vk ..), amelyben a kezdeti csúcs egybeesik x1 végső vk. Ha ez az áramkör az úgynevezett elemi, ha az összes csúcsok különböznek (kivéve a kezdete és vége, melyek egybeesnek). Áramköri egység hossza kialakított ív formában (a, a) nevezzük hurok. Például, ábrán. 2.1 (e, d, c, b) - útvonal (c, e, d, c) - hurok, (d, d) egy hurok.
Egy irányítatlan gráf, illetve, és bevezette a lánc hurok. Chain (ciklus) az úgynevezett Euler. ha átmegy a széleket egyszer. Circuit (ciklus) a Hamilton. ha átmegy minden a gráf egyszer.