Meghatározása rugalmassági modulus hajlító technika - tanulj pár!
Célkitűzés: kísérleti meghatározása a rugalmassági modulusa lemezek különféle anyagokból készülhetnek, a hajlítási módszerrel.
Eszközök és tartozékok: telepítése „Young-modulus”, lemezek, meg a terhelések súlyú 0,05 kg, 0,1 kg és 0,15 kg.
Elemei az elmélet és kísérleti módszer
Az egyes elemek a struktúrák és a gépek gyakran csak hosszirányú erők okoz nekik húzóierheiésse vagy kompressziós.
Angol tudós Robert Guk XVII században fedezték fel az alapvető jog közötti erők és mozgás okozta rájuk vonatkozó arányosan nyúlás a minta a húzóerő.
Angol tudós Thomas Young a XIX század első ízben fejezte ki az ötlet, hogy van egy állandó minden lényeges jellemző, hogy képes ellenállni a külső hatásoknak. A koncepció az ilyen nagyságrendű, amit az úgynevezett (később „Young modulus”), „rugalmassági modulus” fogalmazták 1807 című művében: „Natural Philosophy”.
A rugalmassági modulus ismerteti a legfontosabb tulajdonsága a szerkezeti anyag - merevség - és alapvető fogalom, amely nélkül nem tud semmilyen műszaki számítás szerkezeti elemek és szerkezetek. Ábra. Az 1. ábra egy rúd egy egyenes vonalú tengelye az intézkedés alapján a hosszirányú erők N, ahol
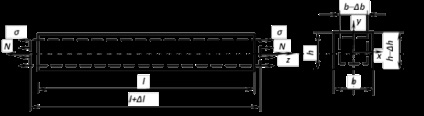
# 963; - névleges feszültség,
A - keresztmetszeti területe a rúd.
Ábra. 1. Hosszanti és keresztirányú alakváltozása a rúd
Az intézkedés alapján hosszirányú erők deformált rúd. Ha meghosszabbodik, annak hossza nő, és egyenlővé válik az L + # 8710; L. ahol # 8710; L - az abszolút hosszanti alakváltozás (megnyúlás) a rúd. A keresztirányú méretei a redukált és értékeket vehetnek H- # 8710; H és B- # 8710; B. ahol # 8710; H és # 8710; B - az abszolút keresztirányú alakváltozása a rúd.
Az arány az abszolút hosszanti alakváltozása a rúd, hogy eredeti hosszának nevezzük a relatív hosszirányú alakváltozás:
Az arány az abszolút oldalirányú deformációját a rúd az eredeti keresztirányú mérete az úgynevezett relatív keresztirányú alakváltozás:
Itt „+” jel a törzs és a „-” jel a deformációkat és továbbítható, mert a szakítási hosszanti méretei a rúd nagyobb és a keresztirányú csökkenés.
Az utolsó lépés a kialakulását Hooke-törvény a jelenlegi formájában a francia matematikus Cauchy, aki 1822-ben vezették be a tudományos irodalomban a „stressz” és a „törzs”, egy francia tudós és Navier, aki 1826-ban adta a meghatározása a rugalmassági modulus, mint az arány a terhelés egységnyi keresztmetszeti területe, hogy a nyúlás, hogy így termelt
Amennyiben E - Young modulus (rugalmassági modulus az első volt).
Így a törvény Hooke kapott gyakorlati alkalmazás formájában a képlet
A rugalmassági modulusa E az anyag egy fizikai állandói és kísérletileg határozzuk meg. Értékét kifejezett ugyanabban az egységben a feszültség # 963;, m. E. pascalban (Pa), például # 949; - egy dimenzió nélküli mennyiség. A rugalmassági modulusa a legtöbb anyag van nagy numerikus értékeket, és ez általában kifejezve GigaPascal (GPa).
Az abszolút értéke az arány a relatív keresztirányú törzs és a relatív hosszirányú törzs húzó vagy nyomó a hatálya alá Hooke-törvény nevezik Poisson-tényező
Ez dimenzió együttható jellemző tulajdonságait az anyag és a kísérleti úton határozzuk meg. Ő névadója a francia tudós, aki először bemutatta őt az elmélet.
Az alkalmazás után a test a külső terhelés ő pont mozog. Jellemzően a nagysága a rugalmas elmozdulást feltételezzük, hogy kicsi a geometriai méretei deformálható testek. Tekintsük például az elmozdulás a konzolos gerenda L hosszúságú unilaterális külső beépülését ábrán. 2. A szabad végén a fény alkalmazzák koncentrált erővel F. amelyek deformálódását okozza annak pont. Lehajlása a sugár ebben a részben jelölik # 948;. Isolate volumentényezőt Dz gerenda hossza. a távolból Z a rögzített vég.
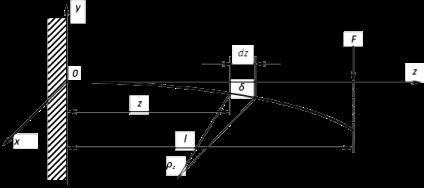
Ábra. 2. hajlítás a konzolos rúd
A deformált állapotban az aktuális szekcióban a fénysugár által leírt görbületi sugarát vagy görbületi ívelt tengely.
Ismeretes [2], hogy az egyenlet a hajlított a fénysugár tengelye a formája:
Ahol IX - axiális tehetetlenségi nyomatéka
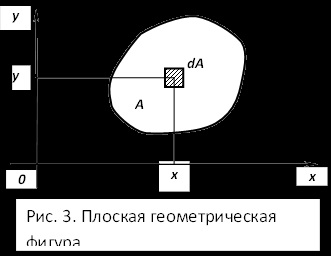
Ábra. A 3. ábra egy tetszőleges keresztmetszete egy lapos geometriai alakzat, amelynek területe A. megkülönböztetni rajta elemi terület DA.
Mi határozza meg a téglalap keresztmetszetű tehetetlenségi nyomaték tengelyére vonatkoztatva CX és CY. a középpontján átmenő, ábrán látható. 4.
Osszuk a téglalap területe elemi téglalap méretei B és Dy. ezen a területen. Behelyettesítve az érték az expressziót (9) és integrálása, kapjuk:
Vegyünk egy gerenda hossza L. szerelt két támogatja és betöltött ábrán látható. 5.
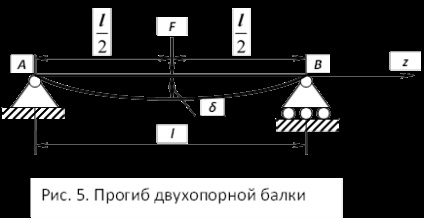
A megoldás a differenciálegyenlet (8) úgy állíthatjuk elő, egymást követő integráció. Amikor a külső terhelés képest szimmetrikusan helyezkedik el a támaszok, ábrán látható. 5, a megoldás ennek egyenlet [2] válik:
Ezért, a Young-modulus képlet határozza meg
Ami a kifejezést (10) megkapjuk
Következésképpen meghatározó F terhelés és az értéke a lehajlás # 948; a gerenda (lemez), L hosszúságú keresztirányú méretei a B és H. általános képletű (14) ki tudja számítani a Young-modulus az anyag, amelyből készült.
Leírás A kísérleti elrendezés
Sematikus ábrázolása a létesítmény „Young-modulus” ábrán látható. 6.
Beállítása „Young-modulus” áll egy alap 1, amely rögzített recepción 2. Keleti konzol 3 két hasáb hordozók 4. A támogatás 5 telepítve a minta (lapka). 7. minta a tölténytár, amely egy prizmatikus tartókonzol, csatolt a minta dial-terhelés 6 és 8 óra indikátor.
Az, hogy a teljesítmény
1. Helyezzük az egyik vizsgálati lemezek a prizmás rátét 4.
2. Állítsa be az órát jelző 8 úgy, hogy a hegye a lemez.
3. Hang hevedernek 7 a lemez közepén.
4. Csatlakoztassa a kengyel Egy tömeg M1 = 0,1 kg.
5. A skálán jelző 8 értékének meghatározásához a terelőlemez # 948; 1.
Hang a kengyel 7. Egy tömeg M2 = 0,15 kg.
8. skálán jelző 8 értékének meghatározásához a terelőlemez # 948; 2.
9. Számítsuk ki a F terhelés, amelyet a képlet
Amennyiben G - a gravitációs gyorsulás.
10. Az érték a terelőlemezek definiált
11. Keresse meg a Young-modulus az (14) képletű, ahol L = 0114 m - távolság a prizmák között (hossza lemez); B = 0,012 m - keresztmetszeti szélessége a lemez; H = 0,0008 m - a lemez vastagsága; # 948; - az érték a terelőlemezek, m.
12. lépéseit egy második lemez fölött.
13. Ismételje mindkét rugók állításokat. 1-12 még kétszer.
Az anyag a minta - rugós acél és bronz.
A kapott eredményeket magyarázó rugalmassági modulusz lemezek, hasonlítsa össze őket referencia adatokkal [3, 4].
Az értékelési eljárását a hibák
Tegyük fel, hogy a hiba értékelése értékeit Young-modulusa, amelyet a képlet (14) határozza meg a lemez hosszúsága mérési hiba L (szisztematikus hiba), és az alakváltozást hibabecslése d (szisztematikus + véletlen hiba).
Rögzítse az eredményeket a közvetlen mérés a fenti paraméterek:
B) d =
Rögzítse az eredményeket a közvetett mérések:
Kérdések és feladatok önkontroll
1. Mi a különbség a normál feszültség az érintő?
2. Melyek a képletek, hogy meghatározza az abszolút és a relatív alakváltozás?
3. Mi az értéke az első fajta az úgynevezett rugalmassági modulus?
4. Hogyan Poisson?
5. Mi a rész hajlítási merevsége?
6. Mi a különbség a képletek tengelyirányú tehetetlenségi nyomaték tekintetében OX és OY tengelyek?
7. Melyik képlet fejezi alakváltozás kétszeresen támogatott gerendák?