Maximum jellemzői -, hogyan kell használni a referencia munka ru
Maximum a funkció határozza meg a szélsőérték a funkciót. de további feltételeket adunk.
Használjon kalkulátor találni, legfeljebb a funkciót:
A maximális y = 1 / e, az a pont x = 1
Annak érdekében, hogy megtalálják a szélsőséges, meg kell megoldani az egyenletet $$ \ frac f = 0 $$ (a-származék egyenlő nulla), és a gyökerek ebben az egyenletben a szélsőséges a függvény: $$ \ frac f = $$ Az első derivált $$ - xe ^ + e ^ = 0 $$ megoldja ezt a egyenlet
A gyökerei ennek ur-CIÓ: $$ x_ = 1 $$ jel. szélsőségek pontok:
-1 (1, e)
Időközönként növekedését és csökkenését a funkció:
Találunk intervallumokban, ahol a funkció növekedését és csökkenését, valamint a minimum és a maximum funkciók, ezt keressük függvényében viselkedik szélsőértékében a legkisebb eltérés a szélsőérték:
Louis a funkciót is.
A maximumok a funkció pontot: $$ x_ = 1 $$ pusztuló időközönként
(-OO, 1]
Növeli a hézagokat
[1, oo)
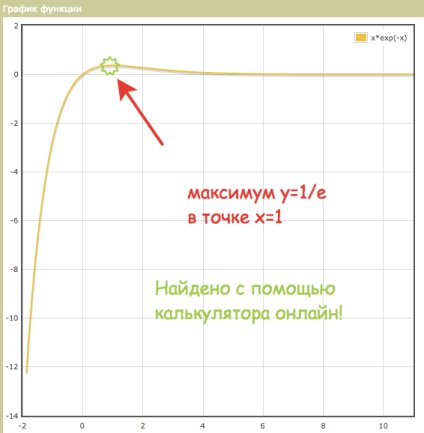
Meghatározott maximális függvény
Maximum funkció - maximális értéke egy adott intervallumban. Maximum a következő:
Ez megoldja az egyenletet. „Függvény deriváltját egyenlő 0” az ismeretlen x (ha a funkció függ x) és úgy néz ki, az eredmények x pontként változó a jele differenciálhányados, áthalad ezen a ponton
Egy másik egyszerű példa a maximum funkciót
Tekintsük az -x ^ 2. Deriváltja egyenlő -2 * x (Mellesleg származék az itt) - az egyenlet megoldásához -2 * x = 0 - akkor x = 0.
Look - -2x származékot ha X> 0 - kevesebb, mint 0, és ha X <0 производная больше 0.
Tehát az x = 0, a funkció -x ^ 2 amelynek legnagyobb. Itt egy egyszerű példa.