MATEMATIKAI álokoskodás

Matematikai paradoxon lehet meghatározni, mint az igazság. annyira ellentétes tapasztalatunk, az intuíció és a józan ész, hogy nehéz elhinni, még azt követően, hogy lépésről lépésre nyomon követni az összes bizonyítékot. Matematikai álokoskodás úgynevezett nem kevésbé meglepő kijelentéseket bizonyíték arra, hogy, ellentétben a bizonyítékok paradoxonok hazugság rejtett, és néha egészen finom hibákat. Mindenesetre a matematika területén - az egyszerű számtani a modern halmazelméleti topológia - megvan a psevdodokazatelstva, azok álokoskodás. A legjobb ilyen érvek gondosan álcázott hiba lehetővé teszi, hogy jöjjön a leghihetetlenebb megállapításokat.

Az első tévedés rendkívül elemi. Mi előzi meg mulatságos paradoxon, példáját, amely a nagy német matematikus David Hilbert tetszett, hogy ismertesse a szokatlan tulajdonságai a legkisebb ordinals „aleph nulla.” Miután a tulajdonos egy csodálatos szálloda, mely végtelen, de megszámlálhatatlan szállodai szobák, melyek közül egyik sem volt szabad, szükséges volt, hogy fogadjon el egy új vendég. A tulajdonos kijött a helyzet nagyon egyszerű: minden a vendégek, s áthelyezték a szobában, ami eggyel nagyobb, mint az előző szám a szoba, így n-edik lakója a szoba költözött az (n + 1) -edik és kiadta a legelső új vendég szobában. Hogyan lehet egy földesúr tenni, ha megérkezik végtelenül sok új vendégek? Nem összetéveszthető a fogadó áthelyezi az összes korábbi vendégek kétágyas szobák nagy számban (a vendég a szoba 1 mozog a szobában 2, a vendég a szoba 2 - szoba 4, a vendég a szoba 3 - szoba 6, a vendég a szoba 4 - in terem 8, és így tovább. d.), és elhelyezi az újonnan érkezők a felszabadult szobák páratlan számok.

De meg kell, hogy a tulajdonos egy megszámlálható szobaszám elhelyezése érdekében új vendégek? A Stishov alábbi vett egy brit magazin, megjelent a múlt században, azt mondja a ravasz fogadós, aki képes volt befogadni kilenc szoba tíz vendéget, hogy azok mindegyike kapott egy külön szobában.

Voltak tíz különcök,
Azok műholdak fáradt,
Ez úgy döntött, hogy kopogtattak az ajtón,
Vendéglők „kedves srác”.

- Engedj, mester, benyújtani,
Nem lesz veszteséges,
Mi csak egy éjszaka aludni,
Mi áztattuk a bőrt.

A tulajdonos a vendégek örültek
De a baj a helyén:
Csak kilenc szoba is
És csak kilenc ágy.

- fogom ajánlani nyolc vendég
Ágynemű becsület a becsület,
És a kettő átaludni az éjszakát
Ugyanebben ágyban.

Csak mondta, és azonnal sírni
Düh vörös arc:
Nem egy mind a tíz
Nem akarja, hogy legyen hely.

Milyen jó a szenvedélyek a buzgalom,
Mérsékelt is izgalom?
De a régi szélhámos tulajdonos
Vagy kétség.

Az első két utazó még
Annak érdekében, hogy ne kell megítélni súlyosan,
Azt kérte, hogy menjen az „A” szám
És várjon egy kicsit.

Aludtam a harmadik a „B”, a negyedik a „B”
A „G” aludt egész éjjel, az ötödik,
A "D", "E", "F", "3", B talált
A hatodik és a kilencedik.

Ezután visszatért a „A”
Ahol várta a két,
Ő a legfontosabb, hogy az „én” boldog volt, hogy
Tizedik hős.

Bár sok év telt el azóta,
Nem világos, hogy bárki,
Hogyan lehetne a mester poszt
A vendégek egyenként.

Ile számtani régi
Vagy egy csoda előttünk,
Ahhoz, hogy megértsük, mit, hogyan és miért,
Megpróbál tenni.

Egy példa a vékonyabb az alábbi matematikai szofizma „algebrai„bizonyítja, hogy tetszőleges számú, valamint egy kisebb szám b.

Kezdjük az egyenlőség

Megszorozzuk mindkét oldalán a - b. megkapjuk

Transzfer az ász a bal oldalon:

és számításba:

Elosztjuk mindkét oldalán a - b - c. talál

QED.

Sok bajt várja az, aki véletlenül utal, hogy a képzetes egység i (a -1 négyzetgyöke). Ezt bizonyítja az legalább a következő meglepő „bizonyíték” az egyenlőség 1 = -1:

Ábra. 82. Triangle Kerry.

A síkrajzi legtöbb hamis bizonyítékok felhasználásával kapcsolatos helytelen rajzokat. Vegyük például, a csodálatos „bizonyíték”, hogy az első oldalon sokszög területe. kivágott papír eltér a terület a hátsó oldalán egy sokszög. Ez a „bizonyíték” alkotta pszichiáter L. Vosburgh Lyons, hogy használ egy furcsa elvet felfedezett P. Kerry.

Először, hogy felhívja a papírlapot a sejtbe háromszög, amelynek területe egyenlő a 60 sejtek (ábra. 82), és a vágás mentén látható a felső ábrán. Rátérve a háromszög, hogy a másik oldalon, és belőlük egy háromszög ábrán látható. 82 közepén, azt találjuk, hogy a központban az új háromszög lyuk jelent meg a területen 2 sejtekhez. Más szóval, a teljes terület az eredeti háromszög alkatrészek borulás csökkent 58 sejtek! Visszatérve újból (oldallal felfelé), csak a három eredeti háromszög, tudjuk, hogy mind a hat részét az ábra ábrán látható. 82 alatti. Területe megegyezik 59 sejtekben. Valami baj van, egyértelmű, de mi pontosan?

Valószínűségszámítás tele van hihető, de logikailag nem kifogástalan érvelés. Tegyük fel, hogy már találkozott barátjával John, és mindannyian a nyakkendő, hogy a feleséged adott neki karácsonyra. Ha elkezd vitatkozni, akinek nyakkendő drága, és a végén úgy dönt, hogy megy a boltba, ahol vásárolta kapcsolatokat, és megtudja, mennyit mindegyik. Aki nyer (akinek döntetlen lenne drágább) fogadást a feltétellel kell adni a nyakkendőjét vesztes, hogy tompítsa a keserű vereség.

Úgy beszél, mint ez: „Az esélye nyerni és veszíteni ugyanabban rám. Winning, I szegényebbé megfelelő összeg a költségek a nyakkendőmet. Miután elveszítette, én lesz drágább döntetlen. Ezért, hogy egy fogadást. Lennék jobb helyzetben, mint a barátom. "

Természetesen. semmi megállás beszélni John ugyanúgy. Lehet mindkét oldalon tett fogadást, megvan az az előnye egymást?

Az egyik legimpozánsabb topológia paradoxon abban rejlik, hogy a tórusz (fánk felület), ha a felület nyúlik (nem tépi során) lehet kifordítva bármely tetszőlegesen kis lyuk. Nincs probléma itt. De ha a tórusz valóban lehetséges, hogy kifordítja, meg kell figyelni, hogy egy újabb, talán még inkább figyelemre méltó tény.

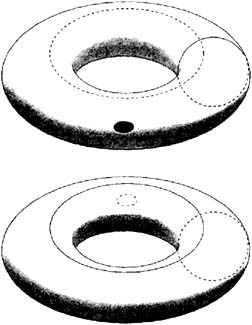
Ábra. 83. Ha a tórusz kifordított, úgy tűnik, hogy a gyűrűk festett felület, elengednek.

A külső oldalán a tórusz felhívni meridián (ábra. 83, top). A belső oldalán az azonos tórusz magatartás párhuzamos. Mindkét körök nyilvánvalóan kapcsolódik egymáshoz. Csavarja ki most a tórusz kifordítva egy lyukon át a felületet. Amint látható az alacsonyabb érték, az első kör gurul befelé a külső felülete a tórusz, és a másik - a külső, és mindkét körök kerül kioldott! Nyilvánvalóan. hogy az sérti az alapvető topológiai törvény, amely kimondja, hogy: külön a két összekapcsolt zárt görbe csak egyet is eltöröl a görbék, és húzza át a szakadékot a második helyen.

A legutóbbi szofizma, amelyet kivett az elemi számelméleti, akkor a viszonylagos érdemeinek „érdekes” számokat. Természetesen. számok érdekesek lehetnek különböző nézőpontokból. Tehát, George Moore, amikor megírta híres óda a nő harminc, tematikus száma volt 30 - Moore gondoljuk, hogy ebben a korban, a házas nők számára különösen vonzóak. A szakértő a számelméleti képviseli a 30-as szám jelenik meg. még érdekesebb, mert ez a legnagyobb a számok, a tulajdonság, hogy minden alacsonyabb szám, amelynek nincs közös tényező velük, pro-ól. A szám 15873 is érdekes: amikor megszorozzuk az alvás-Chal bármilyen alak, azaz, bármely a számok 1-9, majd a 7, akkor az eredmény áll ismétlések kiválasztott első szaporodása a számokat. Meglepő tulajdonságok számos 142 857: megszorozva a számok 1-6, akkor kap egy ciklikus permutációja a hat számot.
Felmerül a kérdés, hogy vannak-e érdektelen számok? Segítségével elemi indokolása nem nehéz bizonyítani, hogy nincs érdektelen számokat. Ha unalmas számok vannak, akkor az összes számot lehetne két csoportba sorolhatók: a számos érdekes és neinte-esting, unalmas számokat. A különböző érdektelen szám lenne egy számot, ami a legkisebb az összes érdektelen számokat. De a legkisebb az összes érdektelen szám - ez a szám önmagában is érdekes. Ezért lenne szükség, hogy távolítsa el a beállított érdektelen számok és lefordítani egy másik. A többi meg, viszont találta volna a legkisebb számot. Ezt az eljárást ismételve sokáig, érdekes lehet bármilyen belső érdektelen számát.

A legnagyobb gond az olvasók nyilvánított álokoskodás a kifordított tórusz. Thor tényleg lehetséges, hogy kifordítja, de megváltoztatja irányát. Ennek eredményeképpen mindkét kör felcseréljük és maradnak elkötelezettség. Ha levágja az alsó része a harisnya és varrni a végén a cső, körökre Khodnev Ez meghaladja a tórusz modell. Ez szálak különböző színű lehet pro-lash hosszúsági és párhuzamos. Az ilyen tórusz könnyen be egy lyukon keresztül a felület, a tökéletesen tiszta minden-prois sétál a meridián és párhuzamos.

Algebra - Az egyik nagy terület a matematika, tulajdonosa együtt számtani és geometriai legrégebbi ága ez a tudomány. Célok és módszerek A. megkülönböztetik más ágak matematika jöttek létre fokozatosan, kezdve az ősi időkben. Algebra keletkezett hatása alatt igényeit a társadalmi gyakorlat, mint egy keresés eredményeként közös megoldási módjait, számolási feladatokat azonos típusú. Ezek a technikák általában a készítményben és egyenletek megoldása. Ie algebrai álokoskodás - szándékosan rejtett hibákat az egyenletek és numerikus kifejezéseket.
1. „Két különböző pozitív egész szám egyenlő”
Mi megoldjuk a rendszer két egyenlet:

Tesszük ezt helyettesítjük a 2. pillanatától 1. egyenlet, megkapjuk x 8 + x = 6, 8, ahonnan da = 6
Hol van a hiba.

2. „A negatív szám nagyobb, mint a pozitív.”
Vegyünk két pozitív szám a és c. Vessük össze a két attitűd:
és / -c és -A / c
Ezek lesz egyenlő, mivel mindegyik egyenlő - (A / C). Tudod, hogy egy részét: a / -c = -a / c
De ha az arány az első ciklus első érték nagyobb, mint később, az első kifejezés a második aránya is nagyobb, mint a következő. A mi esetünkben a> c, a következő képpen kell lennie s> c, azaz negatív szám nagyobb, mint a pozitív.
Amennyiben a hiba.

3. „Kettő meg kettő az öt.”

Jelöljük 4 = 5 = b, (a + b) / 2 = d. Van: a + b = 2d, a = 2d-b, 2d-a = b. szaporodnak az utolsó két egyenletet részein. Kapjuk: 2da a * a = 2db-b * b. Szorozzuk mindkét oldalán a kapott egyenletet -1, és hozzá az eredmények a d * d. Van: egy 2-2da + d2 = b2 -2bd + d2, vagy (a-d) (a-d) = (b-d) (b-d), ahol egy-d = b-d, és a = b, azaz 2 * 2 = 5
Amennyiben a hiba.

Emellett matematikai álokoskodás. van sok más, mint a logika, a terminológia, pszichológiai, stb Ahhoz, hogy megértsük az abszurd az ilyen állítások könnyebb, de nem kevésbé érdekes ebből. Túl sok néz ki, mint álokoskodás mentes értelmét és célját a játék a nyelv; játék alapján a kétértelműség nyelvi kifejezések, azok hiányos, kifejezés, körülményeitől függ az értékek, stb Ezek sophistries látszik különösebben naiv és komolytalan.

„Félig üres, félig tele”
„Félig üres ugyanolyan, mint félig tele van. Ha két egyenlő részre, azt jelenti, és egész számok. Ezért üres ugyanaz, mint a teljes. "

„Páros és páratlan”
„5 jelentése 2 + 3 ( "két és három"). Két - a szám páros, három - páratlan, úgy tűnik, hogy az öt - ez a szám, és a páros és páratlan. Öt nem osztható két, valamint a 2 + 3, akkor a két szám nem a páros! "

„Nem tudom, hogy mit tud”
„Tudod, mit akarok kérdezni?” - „Nem”. - „Tudod, hogy az erény a jó?” - „Tudom.” - „Ez az, amit meg akartam kérdezni. És te, kiderül, hogy nem tudja, amit tud. "

„Gyógyszerek”
„A megoldás által elfogadott beteg, jó. Jót több jobb. Tehát, ha kell szednie, amennyire csak lehetséges. "

„A leggyorsabb lény nem képes felzárkózni a leglassabb”
Gyors lábú Achilles soha nem fogja utolérni a lassan mozgó teknős. Amíg el nem éri a teknősbéka Achilles, akkor haladni egy kicsit. Gyorsan leküzdeni ezt a távolságot, de a teknős hagy egy kicsit előre. És így tovább a végtelenségig. Amikor Achilles eléri a hely, ahol korábban volt ez a teknős, akkor meg legalább egy kicsit. de megelőzve.

„Nincs vége”
A mozgó tárgy el kell érnie a fele utat, mielőtt eléri a végét. Aztán meg kell felelnie a fele a másik fele, majd a fele a negyedik rész, stb a végtelenségig. A téma lesz folyamatosan közeledik a vége pont, de ez soha nem éri el.

A nagy tömegű kis, köles, például gabonát ősszel a földre mindig hangot ad ki. Ez áll az egyes magokat a zaj, és így minden egyes szemcse, és a legkisebb részét minden egyes szemcse kell alá, termé-dit zaj. Azonban egyetlen gabona a földre esik teljesen csendes. Következésképpen a földre hulló medimnov gabonát nem kellett volna, hogy a zaj, mert ez áll a több gabona, amelyek mindegyike elhallgat. Még medimnov gabona esik a zaj!

„Lehet-e egy mindenható bűvész létre egy kő, amely nem tudja felemelni?”
Ha nem - akkor nem mindenható. Ha lehet - így van, akkor nem mindenható, mert nem tudja emelni ezt a követ. „Van egy nagy pohár üres Raven?”
Igen. Használjon egy érv. Legyen egy pohár vízzel teli akár fél. Akkor azt mondhatjuk, hogy a pohár félig tele pohár. félig üres. Növekvő mindkét oldalán kétszer, azt találjuk, hogy egy pohár tele van üres üveg.

„Álokoskodás Cratylus”
Dialektikus Hérakleitosz kihirdetett érv „minden áramlik”, kifejtette, hogy ugyanabba a folyóba (a kép a természet) nem léphet kétszer, amikor a beérkező szerepelni fog a következő alkalommal, akkor szivárog a víz egy másik. Tanítványa Cratylus készült jóváhagyásával a tanár egyéb megállapításai: ugyanabba a folyóba nem tud belépni, még egyszer, mert amíg belépsz, már megváltozott.

Evatl álokoskodás vett órákat a szofista Protagorasz, azzal a feltétellel, hogy ő fizeti a díjat csak akkor, ha megnyeri az első eljárás. Diák edzés után nem vette a magatartás egy folyamat, és ezért tartotta magát jogot, hogy nem fizeti a díjat. A tanár azzal fenyegetőzött, hogy panaszt a bíróságon, és azt mondta neki a következőket: „A bírók jutalmaz, vagy fizetni a díjat, vagy nem adható mindkét esetben meg kell fizetnie az első esetben a bíró ítéletet, míg a második esetben, alapján a megállapodást.”. Ez Evatl válaszolt: „Nem, minden más esetben, nem kell fizetnie, ha én megfizetésére ítélték, aztán elvesztettem az első tárgyalást, nem fizetnek, mert a mi megállapodást, és ha én nem ítélték az a díj befizetését, nem tudom. fizetni értelmében a bírósági ítélet. " (Error világossá válik, ha teszünk két különböző kérdést: 1) azt, hogy nem fizet Evatl és 2) hogy az a szerződés feltételeinek végrehajtott vagy sem).

Példák álokoskodás fogalmazott az ókori Görögországban:

„Sitting állt; aki felállt, és a költségeket; Ezért ül megéri. "

„Szókratész - egy ember; Az emberek - nem ugyanaz a dolog, hogy Szókratész; Ezért, Szókratész - valami más. mint Szókratész. "

„Annak érdekében, hogy ne feltétlenül szem, mert anélkül, hogy a jobb szem látjuk anélkül, hogy látta is, balra; kivéve a jobb és a bal, mások nem szemét; így egyértelmű, hogy a szem nem szükséges a megtekintéséhez. "

„Aki hazudik, mondja a kérdéses esetben, vagy beszélnek róla; ha ő beszél a helyzet, akkor nem hazudik; ha nem beszélni az ügyet, azt mondja, hogy valami nem létezik, és lehetetlen, hogy ne csak hazudni, de még gondolkodni és beszélni. "

„Ha valaki azt mondja, hogy hazudik, hogy hazudik, vagy igazat mond?” Az a feltételezés, hogy igazat beszél, ez azt fogja jelenteni, hogy ez igaz. feküdt (erről azt mondja), akkor kiderül, hogy hazudik. Ha hazudik, akkor pontosan az a tény, hogy ő nyíltan beismeri. Kiderül, hogy ő igazat mond. "

Példák a modern álokoskodás:

„Egy és ugyanaz a dolog nem lehet olyan tulajdonság, és nincs meg. Költségelszámolási feltételezi a függetlenség, az elkötelezettség és felelősség. Az érdeklődés - ez nyilvánvalóan nem a felelősség, és a felelősség - nem függetlenséget. Kiderült, ellentétben azzal, amit az elején mondtam, hogy tartalmaz egy önhordó függetlenség és a függetlenség hiánya, a felelősség és felelőtlenség. "

„Részvénytársaság kapott, ha a hitelt az állam, most nem kellett volna, mert más volt: az ő uralkodása nem volt, azok közül, akik alkalmazni a kölcsön.”