Másodfokú egyenlőtlenségek
Másodfokú egyenlőtlenségek. grafikus módszerrel
Másodfokú egyenlőtlenségek.
Szögletes fogják hívni az egyenlőtlenséget a következő formában:
vagy.
Megjegyzés: Az egyenlőtlenség jele lehet bármely alapvető jele annak, hogy a másodfokú egyenlőtlenség hogy míg a nulla másodfokú polinom.
Ez a cikk lesz szó több módszer Másodfokú egyenlőtlenségek és mutatja az összefüggést ezek a módszerek.
I. módszer A fő grafikus.
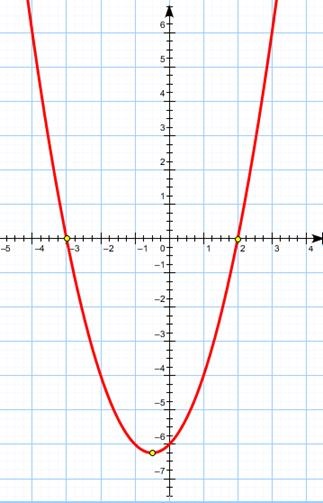
1. példa: oldja az egyenlőtlenséget. A bal oldalon van a másodfokú trinomiális. Construct a menetrend, azaz függvény grafikonját. Mindenki tudja, hogy a grafikon egy másodfokú függvény egy parabola.
Megjegyzés: Az algoritmus a vázlatos felépítését parabola:
1) határozza meg az irányt az ágak.
Ha az ág felfelé és lefelé, ha.
Abban az esetben - az ágak felfelé irányuljon.
2) Határozza koordinátáit metszi a grafikonon az x-tengelyen. Az ordináta az ezek a pontok 0, azaz, függvényében kell helyettesíteni, és oldja meg a kapott egyenletet.
Abban az esetben:
Így a függvény grafikonját metszi az x tengely a pontokat a koordinátákat.
Megjegyzés: Ha egy másodfokú egyenlet nincsenek gyökerei, a parabola keresztezi az x-tengely nem.
3) opcionális tétel, ha a parabola metszi a vízszintes tengelyen a grafikon.
Határozza meg a koordinátákat a csúcsa a parabola.
Abban az esetben:
csúcskoordinátáinak.
Készítünk egy parabola, tényeken alapuló elő:
Emlékezzünk vissza, hogy a probléma megoldódott
Kezdeti egyenlőtlenség felírható: hol.
Határozat a abszcisszán (koordináták) pontok a grafikon, az ordináta (koordináták) nagyobb, mint nulla, azaz fekszenek a felső felében. Hadd magyarázzuk meg ezt a kijelentést egy példát.
Példa (egy speciális esete):
Vegyünk egy ponton (lásd. Ábra.) A koordináta.
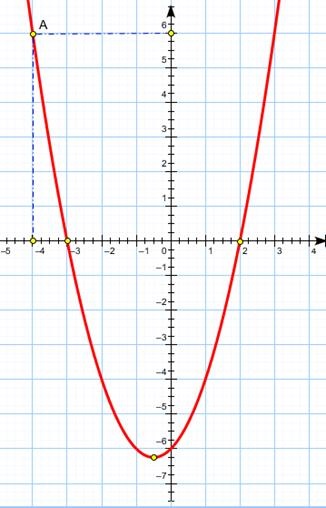
Ez fekszik a felső félsíkban, azaz annak abszcissza a megoldást a egyenlőtlenség.
Nézd meg:
a) A algebrai szempontból:
Helyettesítő egyenlőtlenség:
Az egyenlőtlenség igaz, akkor a megoldás az egyenlőtlenség.
b) A geometriai szempontból. Ne feledje, hogy épített egy parabola, és tartják a pont az abszcissza. Kiszámítjuk az ordináta. . Az ordináta ezen a ponton pozitív, hogy a szabad szemmel látható a grafikonon. azaz egyenlőtlenség teljesül.
Meg kell jegyezni, kék az ábrán parcellákon a grafikont, amelyre a következő feltételek mellett:
Írunk abszcisszájának pontok (a szükséges részeket abszcissza jelöljük keltetés). Ez lesz a válasz, hogy az egyenlőtlenség.
válaszolni:
2. példa:
Oldjuk meg az egyenlőtlenséget.
Építünk a sematikus parabola
1) ágak irányba.
, parabola ága felfelé irányuljon.
2) A kereszteződés OX.

A parabola metszi a vízszintes tengelyen a pontokat a koordinátákat.
3) a koordinátáit csúcsok:
Koordinálja a csúcsa a parabola:
Építünk a grafikon:
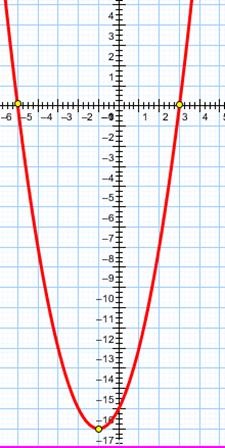
Az egyenlőtlenség felírható hol. Ie megoldások egyenlőtlenség érdekes pontot, az ordináta az, amely kisebb vagy egyenlő nullával, vagyis a fekvő pontok alsó felében vagy OX.
Megjegyzés ezeket a pontokat:
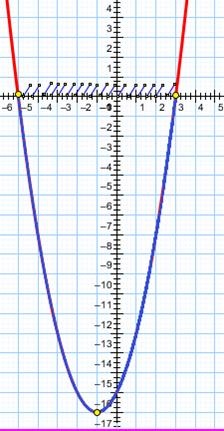
A keltetés jelöli abscissa ezen pontok és írjon egy sor :. Ezek az értékek a változó és lesz megoldás az egyenlőtlenség.
válaszolni:
3. példa:
Oldjuk meg az egyenlőtlenséget.
Építünk a sematikus parabola
1) ágak irányba.
, parabola ága felfelé irányuljon.
2) A kereszteződés OX.
Nem gyökereit.
Parabola metszi az x-tengelyen.
3) A csúcsának koordinátái:
Koordinálja a csúcsa a parabola:
Építünk a grafikon:
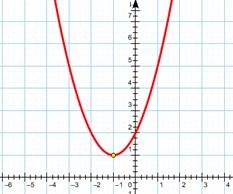
Az egyenlőtlenség felírható hol. Ie megoldások egyenlőtlenség érdekes pontot, az ordináta az, amely kisebb vagy egyenlő nullával, vagyis a Pont fekvő alsó felében, vagy az x-tengelyen. Nincsenek ilyen pontok, minden a parabola felett van az x-tengelyen. Így megfelelő kimenetet.
Válasz: nincs megoldás, azaz a nincs ilyen változó értékeket, amelyeken egyenlőtlenség - jobb.