Markov-láncok
Modellezése gazdasági rendszerek Markov-folyamatok
Alapfogalmak Markov folyamatok
A véletlenszerű funkció nevezzük, ha az értéke, ha lu-bom érv / véletlen változó.
Random függvény argumentuma egy időben, az úgynevezett sztochasztikus folyamat.
Markov folyamatok egy speciális fajtája a pro-véletlenszerű folyamatok. Egy különleges hely Markov-folyamatok között más osztályokba véletlenszerű folyamatok miatt a következő esetekben: Markov folyamatok jól kidolgozott matematikai ap-Paraty, amely lehetővé teszi, hogy megoldja számos gyakorlati problémát; érzelgés-schyu Markov eljárásokat ismertetni lehet (vagy becsülve pontosan-de) viselkedése igen komplikált rendszerek.
Definíció. Véletlenszerű folyamat előforduló ka-Coy vagy S rendszer, ez az úgynevezett Markov-folyamat (vagy eljárás nélkül utóhatás), ha a következő jellemzőkkel bír: minden alkalommal / 0, a valószínűsége bármely állam a rendszer a jövőben (a /> / 0) attól függ, csak annak állapotban a jelen (a / = / 0), és nem függ, hogy mikor és hogyan kell egy S-time rendszer jött ezt az állapotot.
Osztályozása Markov folyamatok. Osztályozás Markov-Ing folyamatok szükségessége attól függ, egy folytonos vagy diszkrét természete folytonosság-beállított értékei függvényében X (t) és a paraméter /.
Vannak az alábbi főbb típusai Markov folyamatok:
• diszkrét államok és diszkrét idejű (Markov-lánc);
• folyamatos és diszkrét idejű állapot (mar-Markov-szekvencia);
• diszkrét állapotok és folytonos idejű (nem-folytonos Markov-lánc);
• folyamatos államok és a folyamatos időben.
Ebben a tanulmányban csak azokat a pro-Markov folyamatok diszkrét állapotok Sb S2 ,. Sn.
C) AF állapotban. Markov folyamatok diszkrét-tartalmazó niyami kényelmesen szemléltetjük az úgynevezett Államok a grafikon (ábra. 2.1), ahol a körök jelzik Államok Si, S2 ,. S rendszer, és a nyilak - a lehetséges átmenetek egy állapotból egy állami ence. A grafikon jelölt csak azonnali átmenetek, és nem mozoghat más államok. Lehetővé költségű részt ugyanabban az állapotban ábrázolják „hurok”, azaz a. E. mutató nyíllal egy adott állam saját magára. Az államok száma a rendszer lehet véges vagy végtelen (de figyelembe NYM). Példa J rendszerállapot grafikon ábra mutatja be a 2.1.
Ábra. 2.1. Gróf rendszer megállapítja, S
Markov-folyamatok diszkrét állapotok és diszkrét idejű Markov-lánc nevezik. Az ilyen pro-átengedésének alkalommal TX. t2 ,. 5, amikor a rendszer tudja megváltoztatni az állapotát-yanie minősülnek egymást követő eljárási lépések és a kitüntetéssel Ka-argumentum, amelyen az eljárás nem nyúlik idő / lépés és az 1. számú, a 2,. Véletlen eljárás ebben az esetben a HA acterized szekvenciája States 5 (0) 5 (1) 5 (2). S (k),. ahol az 5 (0) - A kezdeti állapotban a rendszer (az első lépés előtt); 5 (1) - a feltétele a rendszer az első lépés után; S (k) - a-álló rendszer után N-edik lépésben.
Esemény álló az a tény, hogy miután a k-adik Sha ha rendszer állapotban 5 / (/ = 1, 2) a kis- és NYM esemény. Sequence állapotban 5 (0) 5 (1). 5 (). Meg lehet tekinteni, mint egy sorozat véletlenszerű Søby-rd. Egy véletlen események sorozata úgynevezett Mar-bank láncot, ha nem függ, hogy mikor és hogyan a rendszer-ma jött az 5 / az egyes lépések átmeneti valószínűség Lu-God állapotban 5 / bármikor Sj. A kezdeti állapotban 5 (0) lehet előre pontosan meghatározni vagy véletlenszerű.
A valószínűségek a Markov-lánc a valószínűségek nevezzük öt-Pt (k), hogy miután a K-lépésben (és, mielőtt a (k + 1) -edik) rendszer 5 lesz az állapotban 5, (/ = 1,2. N). Nyilvánvaló, hogy bármely k
A kezdeti valószínűségi eloszlása a Markov-lánc azt jelzi nevezett valószínűségi eloszlása a Államok elején a folyamat:
Abban az adott esetben, amikor a kezdeti állapot a rendszer S pontnál-Ness ismert S (0) = Sh akkor a kezdeti valószínűségi RDO) = 1 és az összes többi nulla.
Átmeneti valószínűség (átmeneti valószínűség) a k-adik lépésben az állam Si, hogy az állam Sj nevezzük a feltételes valószínűsége, hogy az első, az S rendszer, miután a k-adik lépés lesz állapotban, amikor az A yc-lovii, közvetlenül azelőtt (miután k - 1 lépés), hogy on-állam hodilas 5 /.
Mivel a rendszer lehet az egyik N állapotok, majd minden egyes alkalommal / valószínűleg kell beállítani n-stey átmenet Roux, amelyeket célszerűen formájában mutatják be a következő mátrix:
ahol - a valószínűsége, hogy egy átmenet egy lépésben az állam Sj az állam S /, - a valószínűségét a késleltetési rendszer az állam Sj.
A mátrix (2.3) nevezzük egy átmenetifém, vagy átmeneti valószínűség mátrixban.
Ha az átmeneti valószínűségek nem függnek a lépés számát (idő), és csak attól függ a sorrendben egy állam, amelyhez átmenetet hajtjuk végre, a megfelelő Markov-lánc nevezik, a homogenitást.
A átmeneti valószínűségek a homogén Markov-lánc a Ru-alkotnak négyzetes mátrix mérete NxN veszi néhány jellemzőjét .:
1. Minden sor jellemzi a kiválasztott rendszer állapotát és annak elemei a valószínűségek minden lehetséges átmenetek egy következők közül választott lépés (a / th) állapotban, beleértve egy átmenet.
2. Az oszlopok mutatják a valószínűségek minden lehetséges-CIÓ rendszer egy lépéssel egy meghatározott (j-e) állami (más szóval, a vonal utal, hogy a valószínűsége átmenet az állam, az oszlop - a szövetségi állam).
3. Az összeg a valószínűségek minden sorban megegyezik az egység, mint az átmenetek alkossanak csoportot összeférhetetlen események:
4. A fő átlós mátrix átmeneti valószínűségek a valószínűsége, hogy a rendszer ki az állam, és továbbra is azt.
Ha homogén Markov-lánc van beállítva kezdeti valószínűségi EFINITIONS Ras (2.2) és az átmeneti valószínűségi mátrix
(2.3), a valószínűsége rendszer állapotok által meghatározott kiújulásának képlet:
Példa 2.1. Tekintsük a folyamat működését a rendszer, akkor autót. Hagyja, hogy a jármű (rendszer) a CME-HN (nap) lehet két különböző állapotban: helyesbítette Mr. és hibás. Gróf rendszer állapotát ábrán látható. 2.2.
Ábra. 2.2. Gróf autó feltételek
Ennek eredményeként a tömeges megfigyelések av-t o munka összeállított a következő mátrix átmeneti valószínűségek:
a valószínűsége, hogy a jármű jó állapotban maradjon;
a valószínűsége átmenet az állam az autó „javító-vénák” a „hibás”;
a valószínűsége átmenet az állam az autó, „Fault-véna”, hogy az állam „OK”;
a valószínűsége, hogy a jármű továbbra is a „hibás” állapot.
A vektor kezdeti valószínűségek a jármű képes feltenni
Ez szükséges, hogy meghatározzák a valószínűsége, hogy a jármű államok három nap alatt.
Egy mátrix átmeneti valószínűségek, meghatározzuk a valószínűsége-yatnosti Államok Pxx) az első lépés után (az első nap után):
A valószínűségeket az Államok után a második lépés (miután a második sous-áram) a következők:
állapotban valószínűségek a harmadik lépés után (miután a harmadik sous-áram) egyenlő
Így, miután a harmadik napon az autó locat-ditsya jó állapotban valószínűséggel 0,819 a „hibás” állapot valószínűséggel 0,181.
Példa 2.2. A működés során a számítógép lehet tekinteni, mint egy fizikai vatsya rendszer S, ami a vizsgálat eredménye az lehet az alábbi állapotok:
Számítógépek teljes mértékben javítható;
A számítógépnek van egy hiba a memóriában, a Ko
toryh tudja megoldani a problémákat;
-EVM jelentős probléma, és meg tud oldani
korlátozott osztály a problémák;
-EVM teljesen elromlott.
A kezdeti időpillanatban a számítógép teljesen működőképes (felállva-Sx). Számítógépes ellenőrizzük, fix mo-Ments tb t2 időt. ty folyamatok játszódnak le az S rendszer, lehet tekinteni, mint egy homogén Markov lánc három lépést (az első, második, harmadik számítógép ellenőrzi). Mátrix-yatnostey átmeneti valószínűség adja meg:
Határozzuk meg a valószínűsége, hogy egy számítógép állam után három ellenőrzéseket.
állapotban gráfnak van az ábrán bemutatott formában. 2.3. Against kazh-Doy nyilak körülvevő megfelelő átmeneti valószínűség. A kezdeti valószínűségek államok
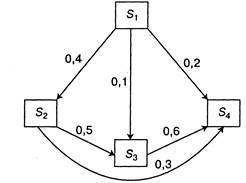
Ábra. 2.3. Gróf számítógép államok
A képlet szerint (2.5), figyelembe véve az összeg a valószínűségek csak azok álló, akiről tudja irányítani átmenet ebben az állapotban, azt találjuk:
Tehát a valószínűsége, hogy egy számítógép állapotban van, miután három ellenőrzés trail-útmutatók: