locus
Az egyik módszer a problémák megoldására az építőiparban a helyek módszere.
Pontok helye nevezzük a szám magában foglalja az összes pont a síkon, bizonyos tulajdonságaikat.
Például egy kört lehet meghatározni, mint a pontok helye egyenlő távolságra egy adott ponton.
Fontos azon pontok helyét adott az alábbi tétel:
A pontok helye egyenlő távolságra a két adatpont egy egyenes vonal merőleges a összekötő szakasz ezeket a pontokat és áthatol a közepén.
Bizonyítás. Legyen A és B - az adatok pont, és - egy sor közepén áthaladó O az AB szakasz merőlegesen (105. ábra). Meg kell bizonyítani, hogy:
1) minden egyes pont a vonal, és egyenlő távolságra a pont, A és B;
2) minden egyes pontja a D síkon egyenlő távolságra pont a B, és fekszik a vonalon.
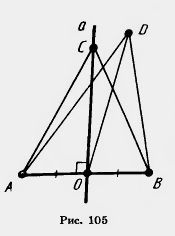
Az a tény, hogy minden egyes egyenes és C pont egyenlő távolságra a A és B pontok, a egyenlőségét háromszögek BOC és AOC. Ezekben a háromszögek a szögek a tetején a közvetlen, teljes működési oldalán, és az AO = OB, mivel a G - a felezőpontja AB.
Most azt mutatják, hogy minden pont D sík egyenlő távolságra a A és B pontok, és fekszik a vonalon. Tekintsük a háromszög ADB. Ő egyenlő szárú, mivel AD = BD. Ez DO - medián. By ingatlan egy egyenlő szárú háromszög a súlyvonal a bázis magas. Ezért, a D pont fekszik egy egyenes vonal. Ez azt bizonyítja, a tétel.
A. V. Pogorelov, geometria évfolyamon 7-11 tankönyv oktatási intézmények
Ha javításokat és javaslatokat a leckét, kérjük lépjen kapcsolatba velünk.
Ha azt szeretnénk, hogy a többi beállítást és javaslatokat órák, nézd meg itt - Oktatási fórum.