Lineárisan konstruktív rajza piramis - építészeti rajz képviseleti
Tudjon ábrázolják piramis különböző pozíciókban.
Döntetlen a kocka a sarokban távon. Építsen minden téren a bázis a kocka függőleges és vízszintes piramis.
Vegyünk például egy piramis látható. 3,43 és merőleges vetülete ábrán. 3.44. Az alapja egy tetraéderes piramis egy négyzet. oldalfelületén - az azonos háromszögek. A magassága a piramis az alaphoz képest oldalán a tér meghatározza annak arányát (magas vagy guggolás).
Kezdeni az építőiparban a piramis kell állnia egy négyzet alapú képet. Keresztül a metszéspontját átlók vertikális ellop, amely félre egy szegmens egyenlő a magassága a piramis (ábra. 3,45). Kombinálása így kapott csúcsa egy piramis négyzet alapú csúcsok kapjunk perspektivikus rajza négyoldalú piramis (ábra. 3,46). Az építés egy piramis négyzet függőleges bázissal hajtjuk végre ugyanabban a sorrendben.
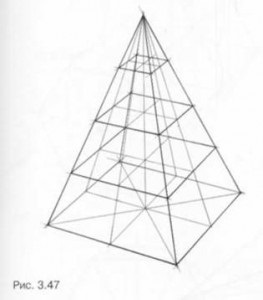
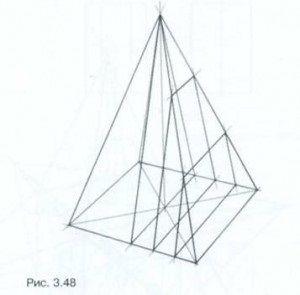
Piramis keresztmetszeti sík párhuzamos az alappal, - négyzetek, amelyek méretben függ a helyzetét a vágási sík - közelebb van a tetején a piramis méret a keresztmetszetek kisebb, mint az alsó (ábra 3.47.). A keresztmetszet merőleges az alapja a piramis, amely átmegy annak vertex és átlagos négyzetes alapvonal, egy háromszög. Minden más szakaszainak a piramis vele párhuzamosan - trapéz, amely egyenlő a nagyobb alapja oldalán a tér bázis minimális - függően változik a helyzet a keresztmetszeti síkban (ábra 3.48.). Az építési ilyen szakaszok ne feledje, hogy az oldalán a trapéz párhuzamos a magasból a háromszögek az oldalsó felületek.
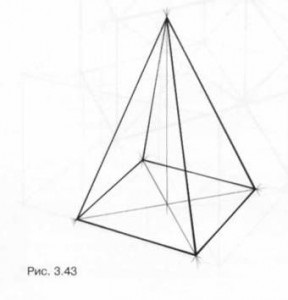
Lineárisan konstruktív rajz piramisok
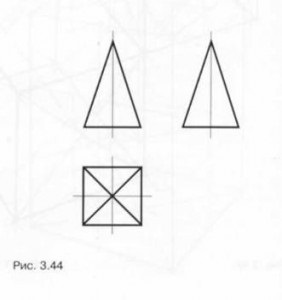
Lineárisan konstruktív rajz piramisok
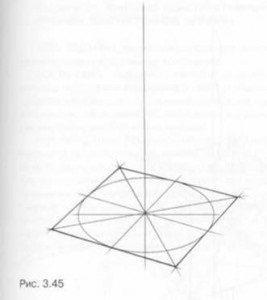
Lineárisan konstruktív rajz piramisok
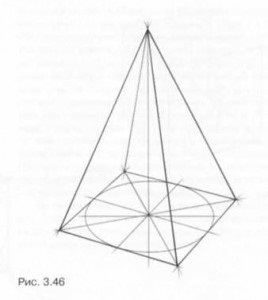
Lineárisan konstruktív rajz piramisok
Lineárisan konstruktív rajz piramisok
Lineárisan konstruktív rajz piramisok
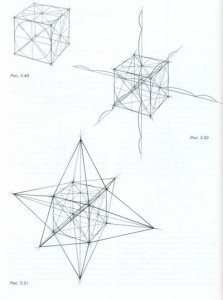
Most, hogy már alaposan tanulmányozták a sorozat építőiparban a piramis és síkokban különböző irányokba, folytassa az alapfunkciók feladatokat. Döntetlen a kocka (ábra. 3,49). Kereszt átlósan mind a hat arcok a kocka, és felhívni egy összekötő vonal a központok szemközti négyzetek. Tedd fel ezeket a sorokat a magassága a piramisok (ábra. 3,50). Mind a hat piramisok azonos magasságban (1.5a, ahol a - szélén a kocka), de ez a szám a magasságuk különböző méretben. Annak megállapításához, a magassága a piramis különböző rendelkezések a különböző szegmenseket alkalmazunk, mint a mértékegység. Például, a meghatározó függőleges magassága a piramisok egy mértékegysége a függőleges vonal szegmensben korlátozott pontok által vízszintes középpontjai kocka arcok. A magassága a vízszintes piramisok ilyen egységek szegmensek egyenes vonalak középpontján átmenő a kocka, és ugyanabban az irányban, mint a meghatározott magasságba. Tehát minden olyan alak, amelynek alapja a geometriai test, működik, mint egy kocka alakú háromdimenziós vonalat, amelynek a segítségével lehet meghatározni, vagy mérésére szegmensek hossza fekvő három egymásra merőleges irányban. Meghatározása az a pont csúcsai a piramisok, is figyelembe hosszú távú csökkentési szegmensek. Csatlakoztassa a tetején a hat piramisok csúcsai indokok négyzetek (ábra. 3,57).
Lineárisan konstruktív rajz piramisok