Lineáris frekvencia moduláció (LFM)

előző ◈ a következő

rádió impulzusok (a 12. ábrát) használnak a gyakorlatban, amelynek gyakorisága a lineárisan változó:

ahol - a frekvencia eltérés,  - impulzus időtartama. Frekvencia-tartományok otdo. Fázis modulációs jel

Átlagos időtartama rezgési frekvenciája. Száma periodovTo hosszasan

jelentése

. A mélysége frekvencia moduláció.

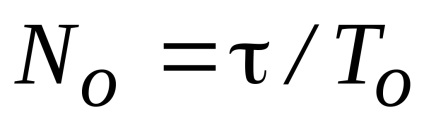
A fő paramétere ciripelésre jel a bázis, amely egyenlő a termék a 12. ábra. Csipog jel dlitelnostina deviatsiyuf 3:

A spektrum a rezgések (13. ábra) meglehetősen bonyolult. Ez fejeződik ki a speciális funkciók - Fresnel integrálok. Annak a ténynek köszönhetően, hogy a megfelelően (48), a fázis  (t) egy még funkció, az összes komponenst a spektrum van egy egyenletes elosztásban chastotyo (1. táblázat, 1.2 verzió).

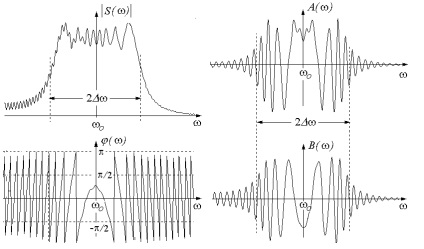
13. ábra. A spektrum a bázissal chirp jel B = 15 és

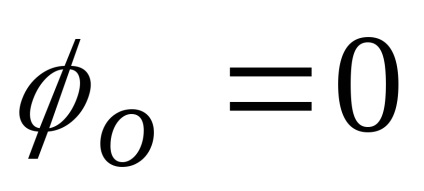
S modul () po alakú trapéz, amelynek a szélessége a magasság felénél mért egyenlő 2. és lejtők meredekebb, mint a nagy bázis. A fázis spektrum által leírt képlet

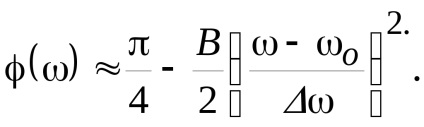
Chirp jelek széles körben használják a rendszerek optimális vételi távolságban radar, és ezért fontos szerepet játszik a autokorrelációs függvény, a borítékot, amelynek az alakja közel van egy funkció (lásd 14. ábra) 4. egy lebeny szélessége

Belül a központi lebeny szélességét 2t ukladyvaetsyaN periodovTo vivőfrekvencia rezgések:

Ha 1 >> A központi lebeny szűk korrelációs csúcsot. Az arány az úgynevezett a tömörítési arányt.

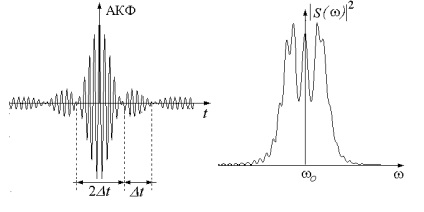
14. ábra. A autokorrelációs függvény a csipogó jelet (a) és annak spektrum (b)

2.4. Amplitúdó-szög modulációs (Aum)

Amikor AUM szerinti (1) és (2) a jel felírható

Ha a függvény F (t) periodikus periodomT = 2. leírható a Fourier-sor komplex amplitudamiFn frekvenciák:

Ezt a rekordot is értelmezhető összegeként harmonikus

, amelyek mindegyike modulált signalomU (t). miáltal spektrU () át a frekvencia

, amely körül voznikayutpartsialnye spektrumok. A teljes tartomány egyenlő az összegük

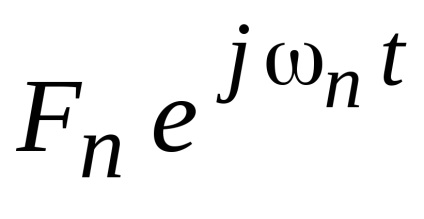
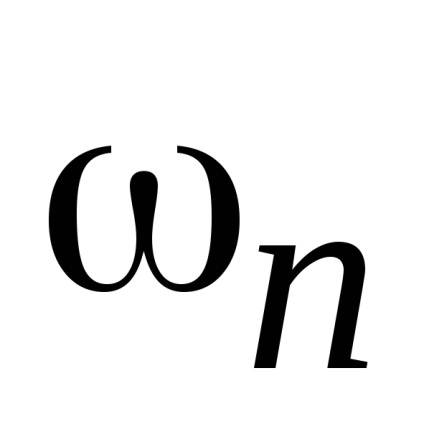
Ha az azonos időszakban T, időzítés és amplitúdó, akkor lehet képviseli a Fourier-sor komplex amplitudamiUm:

van egy részleges frekvencia felharmonikusok eredményül kapott spektrumot. Számuk

Tekintettel a spektrum meglehetősen bonyolult. Különös esetekben, amikor változó a szimmetria funkciók U (t) i (t) az 1. táblázatban leírt. Példa jel periodikus funktsiyamiU (t) i (t) mutatjuk a 15. ábrán.

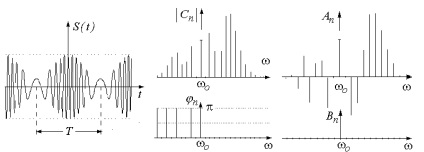
15. ábra. Aum jel (a) és annak spektrumok (b, c) a

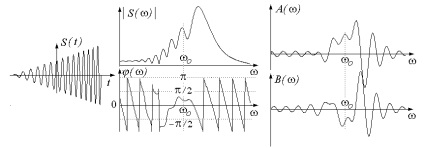
16. ábra. Egységes Aum jel fűrészfogas AM

és lineáris FM bázissal = 5

Bizonyos esetekben lehetőség van arra, hogy egy hasonló értékelést a jel spektrumát. Például, a 16. ábra látható, hogy a modul a spektrális sűrűség növekszik szinte lineárisan növekvő frekvenciával, ami megfelel a növekedés a jelenlegi jel rezgési amplitúdóját csökkenő időtartama a jelenlegi időszakban.

Kapcsolódó cikkek

előző ◈ a következő