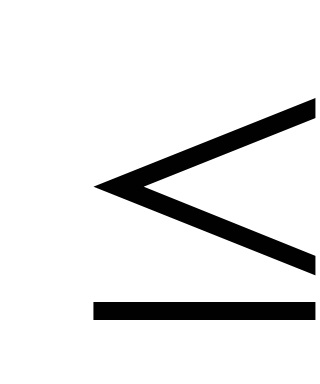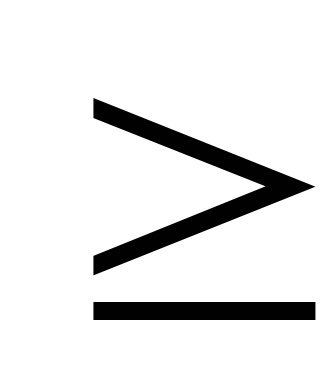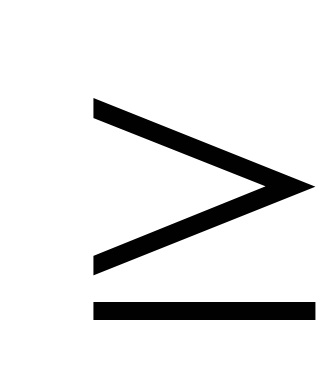Lecture 6 (gradiens módszer)
Gradiens módszerek nemlineáris programozási feladat.
Kérdések: 1. Általános jellemző módszerekkel.
2. Módszer gradiens.
3. Az eljárás legmeredekebb származású.
4. Módszer Franca Fulfa.
5. Az eljárás büntetés funkciókat.
1. Általános jellemző módszerekkel.
Gradiens módszer közelítő (iteratív) módszerek nemlineáris programozási feladat, és megoldani szinte bármilyen problémával. Azonban a meghatározott helyi szélsőérték. Ezért ajánlatos ezeket a módszereket megoldására konvex programozási feladat, amelyben az egyes helyi szélsőérték is globális. A folyamat probléma megoldása áll az a tény, hogy, kezdve egy bizonyos ponton x (kezdeti), a fokozatos átmenetet végezzük irányban gradF (x), amennyiben meghatározásra kerül, maximális pont és -gradF (x) (antigradient), ha a meghatározott minimális pont és amely a megoldást a problémára. Tehát ezen a ponton lehet a tűréshatáron belül, és annak határán.
Gradiens-módszereket lehet osztani két osztályba (csoport). Az első csoportba a módszerek, amelyekben az összes vizsgált pontokat tartoznak a megvalósítható régióban. Ezen módszerek közé tartoznak :. gradiens módszerrel, legmeredekebb származású, Frank-Wolfe, stb A második csoportba tartoznak eljárások, amelyekben a vizsgált pont nem tartozik a régióváltások. Közös ezeknek a módszereknek az eljárás büntetés funkciókat. Minden módszer büntetés funkciók különböznek egymástól, ahogy a meghatározása „finom”.
Az alapvető fogalmak használják az összes gradiens-módszereket, a fogalom a funkció a gradiens irányát legmeredekebb emelkedés a függvény.
Annak megállapítására, az oldatot gradiens módszerek iteratív folyamat folytatódik mindaddig, amíg:
- vagy grad F (x *) = 0, (a pontos megoldás);
ahol
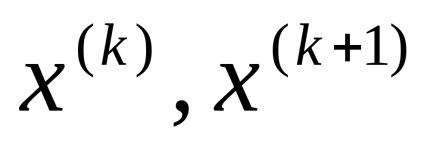
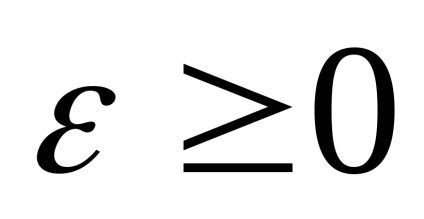
2. Módszer gradiens.
Képzeljünk el egy olyan személy áll lejtőin a szakadék, ami kell, hogy menjen le (alul). A legtermészetesebb, úgy tűnik, az irányában lejtése származású, azaz irányba (-grad F (x)). Kapott ez a stratégia, az úgynevezett gradiens módszer. Ez jelenti a lépések sorozata, amelyek mindegyike két műveletet tartalmaz:
a) meghatározzuk az irányt a legnagyobb meredeksége származású (emelkedés);
b) halad a kiválasztott irányban egy bizonyos pályán.
Helyes pályát kiválasztása elengedhetetlen. A lépés kisebb, annál jobb az eredmény, de több számítást. Különböző módosításokat a gradiens módszer, és áll a használata a különböző módszerek meghatározására pályát. Ha bármilyen lépést F (x) értéke nem csökken, az azt jelenti, hogy a pont „elcsúszott” minimum, ebben az esetben vissza kell mennie az előző pontban, és csökkenti a lépést, például kétszer.
tartozó megvalósítható régió
2. Meghatározás grad F (x 0) vagy -gradF (x 0).
4. meghatározása a következő pont a következő képlet segítségével
x (k + 1) = x (k)
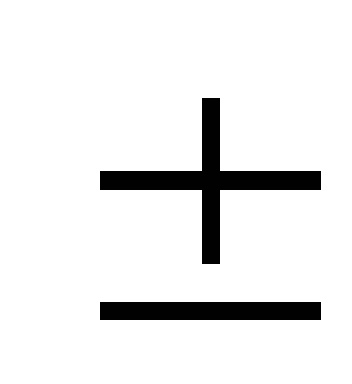
5. meghatározása F (x (k + 1)) és:
- Ha a megoldás talált;
- ha nem, menj., 2. o.
Megjegyzés. Ha grad F (x (k)) = 0, akkor a megoldás pontos lesz.
Példa. F (x) = -6x1 + 2x1 2 - 2x1 x2 + 2x2 2
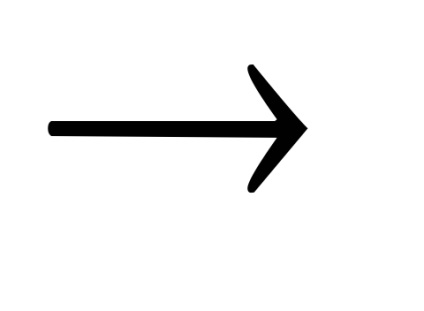
x1 + x2
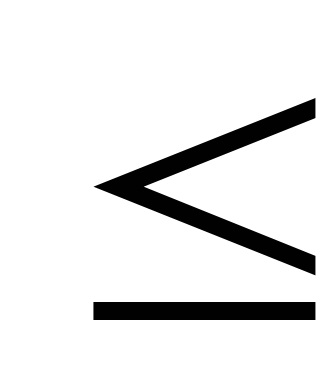
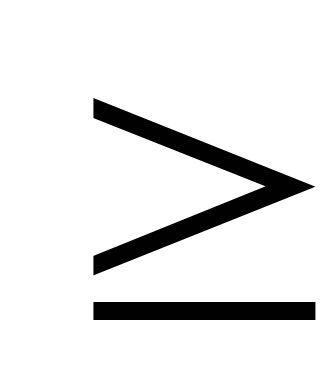
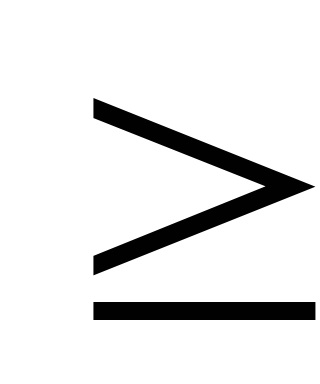

3. Az eljárás legmeredekebb származású.
Ezzel szemben a gradiens módszer, ahol a gradiens meghatározzuk minden lépésben az eljárás a legmeredekebb származású gradiens megtalálják a kiindulási pont és a mozgás iránya eredmények azonos lépéseket folytatni, amíg az értéket a függvény nő (csökken). Amennyiben bármely F (x) lépés növelte (csökkent), a mozgást ebben az irányban leáll, az utolsó lépés teljesen eltávolítjuk vagy részben, és kiszámítja az új értéket a gradiens és egy új irányba.
tartozó megvalósítható régióban,
2. Meghatározás grad F (x 0) vagy -gradF (x 0).
4. meghatározása a következő pont a következő képlet segítségével
x (k + 1) = x (k)
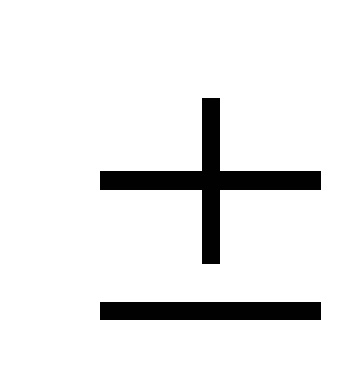
5. meghatározása F (x (k + 1)) és:
- Ha a megoldás talált;
a) a keresett perc: - ha F (x (k + 1)) - ha F (x (k + 1))> F (x (k)) - átmenet a 2. lépéshez ;. b) amikor keres max: - esliF (x (k + 1))> F (x (k)) - lépéssel folytatva 4 ;. - Ha F (x (k + 1)) Megjegyzések: 1. Ha a grad F (x (k)) = 0, akkor a megoldás pontos lesz. 2. Az előnye a legmeredekebb származású módszer egyszerűsége és A kifizetések csökkentése, a grad F (x) kiszámítása nem minden ponton, hogy Fontos nagyszabású problémákat. 3. A hátránya az, hogy a következő lépéseket kell kicsi, hogy ne hiányzik az a pont optimális. Példa. F (x) = 3x1 - 0,2x1 2 + x2 - 0,2x2 2 x1 + 2x2

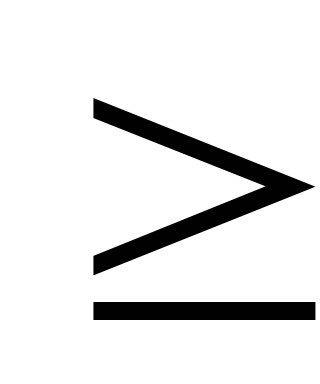
4. Módszer Frank-Wolfe.
A módszert használják, hogy optimalizálja a nem-lineáris célfüggvény lineáris korlátok. A pont szomszédságában egy nemlineáris célfüggvény helyett egy lineáris függvény, és a probléma csökkenti az egymást követő előállítása lineáris programozási feladatok.
1. Meghatározás 0 x = (x1, x2, ..., xn), tartozó régióváltások, és F (x 0), k = 0.
2. meghatározása grad F (x (k)).
3. Egyesítés funkció
4. meghatározása max (perc) f (x) kezdeti korlátok. Legyen ez egy pont z (k).
5. meghatározása számítási lépés x (k + 1) = x (k) +


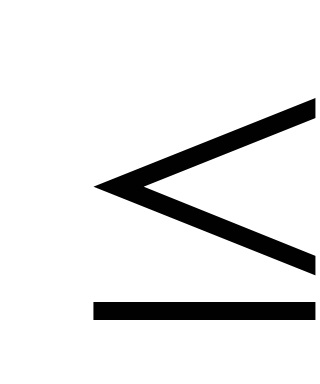

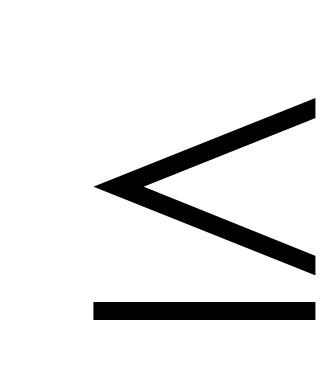

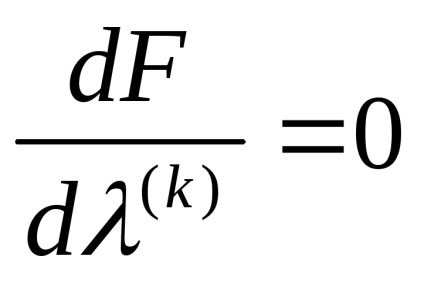
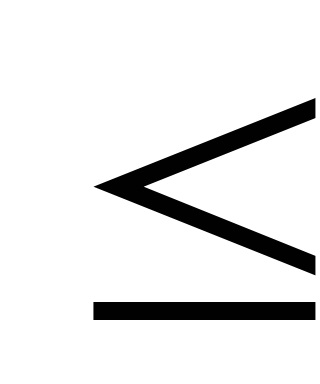

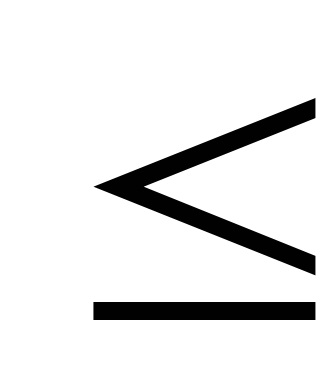
6. meghatározása F (x (k + 1)), és ellenőrizze, hogy szükség van további számítások:
- vagy ha grad F (x (k + 1)) = 0, akkor az oldatot talált;
- ha nem, menj., 2. o.
Példa. F (x) = 4x1 + 10x2 -X1 -X2 2 2
5. Az eljárás büntetés funkciókat.
Tegyük fel, hogy meg kell találni az F (x1, x2, ..., xn)
gi (x1. x2, ..., xn)
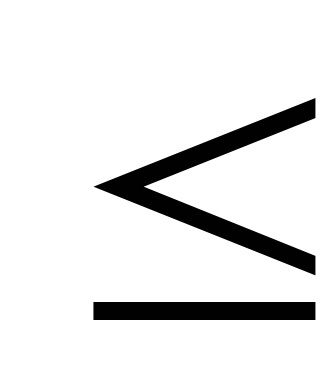
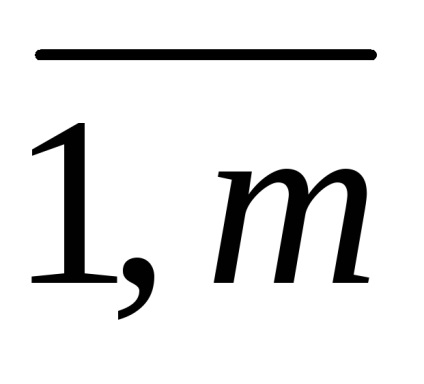
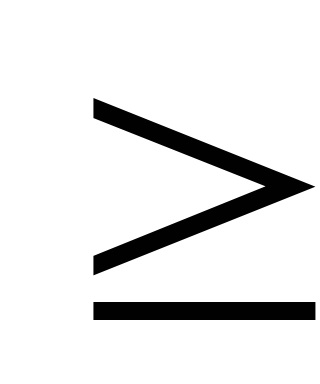
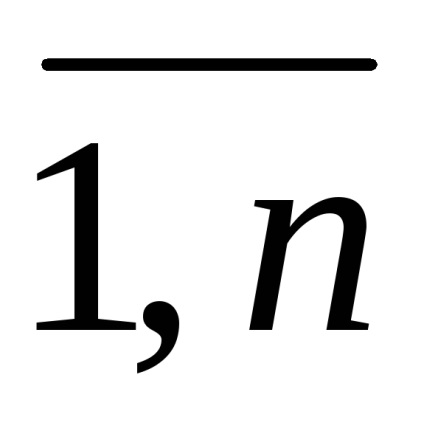
A funkciók F és GI - homorú vagy domború.
Az az elképzelés, a módszer a büntetési függvény, hogy keressen új optimális értékét a célfüggvény Q (X) = f (x) + H (x), amely a összege az eredeti célfüggvény és egy függvény H (x), által meghatározott rendszer korlátai és a hívott büntetési függvény. Büntetés funkciókat épített oly módon, hogy biztosítsa a gyors visszatérést a megengedett tartományon, vagy lehetetlen kijutni belőle. Büntetés függvény módszer csökkenti a problémát egy feltételes szélsőérték a megoldás sorozata feladatok feltétlen szélsőérték, akkor könnyebb. Számos módja van az építési bírság funkciókat. Leggyakrabban ez:
ahol
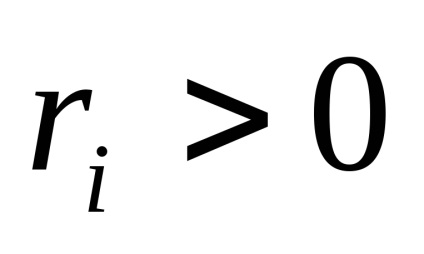
- kevesebb, mint
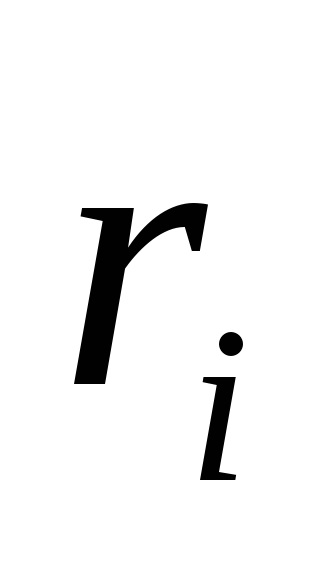
- Először egy kis megoldás
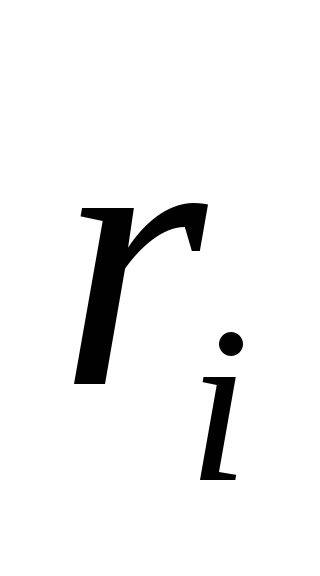
A büntetési függvény, következetesen halad egyik helyről a másikra, amíg, amíg nem kap egy elfogadható megoldás.
1. meghatározása a kezdőpont x 0 = (x1, x2, ..., xn), F (x 0), és a k = 0.
2. Jelölje ki a számítási lépésben h.
3. Határozza meg a részleges származékok
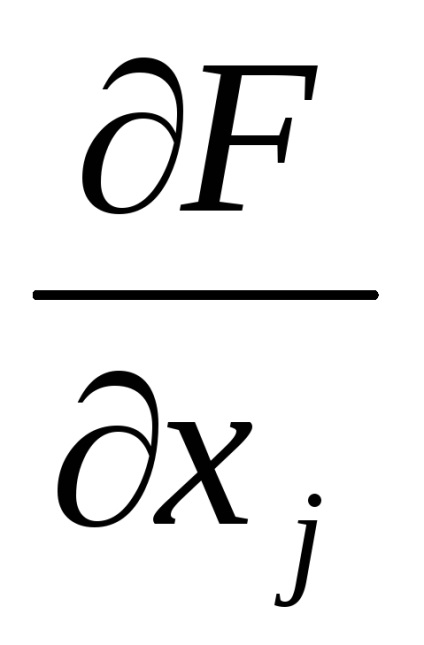
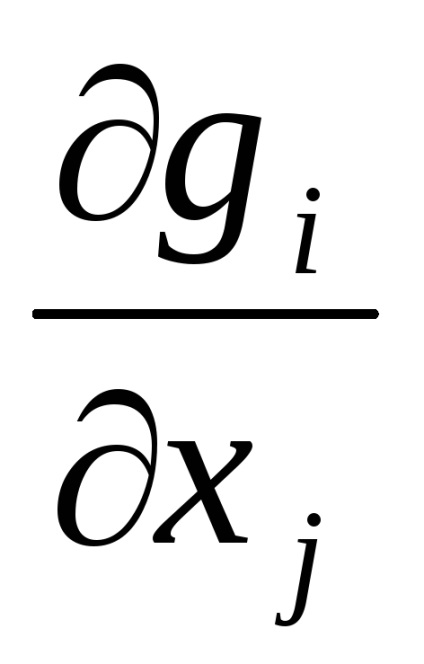
4. Határozza meg a koordinátákat a következő pont a következő képlet segítségével:
5. Ha az x (k + 1)

a) ha - a megoldás, ha van - folytassa a 2 ..
b) ha a grad F (x (k + 1)) = 0, a pontos megoldás.
Ha x (k + 1)

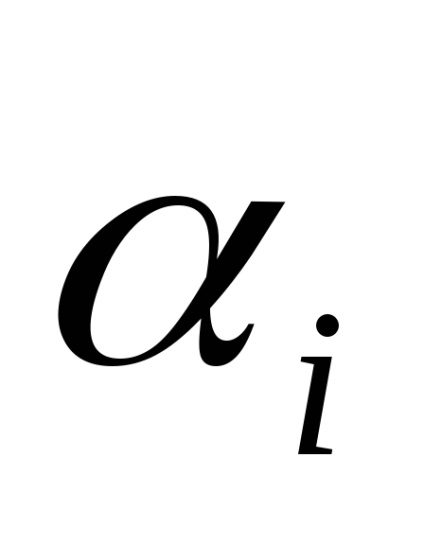
Példa. F (x) = - x1 2 - x2 2
(X1 -5) 2 + (x2 -5) 2