Laplace transzformáció alapmeghatározásait a tulajdonságait a Duhamel képletű - problémamegoldás, kontroll

Alapvető definíciók Laplace-transzformáció tulajdonságai Formula Duhamel

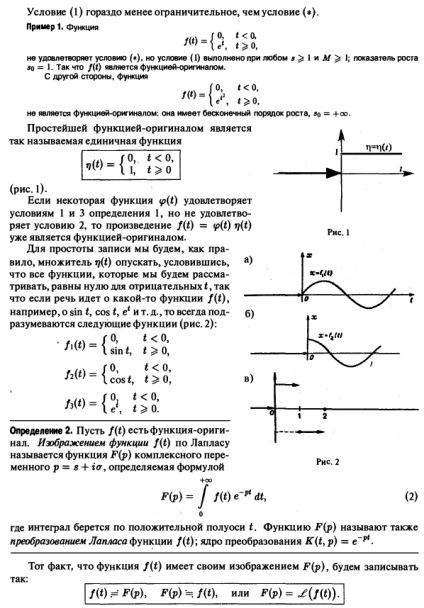
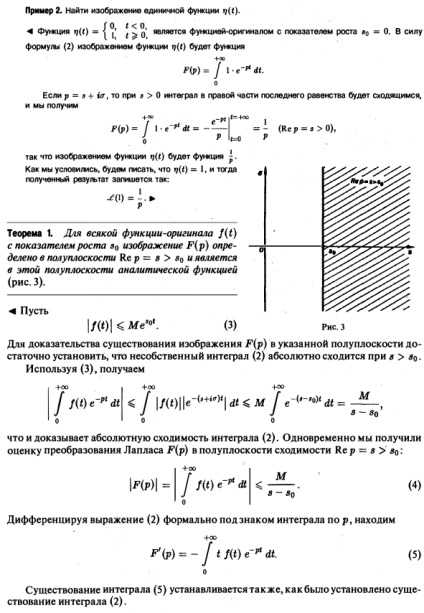
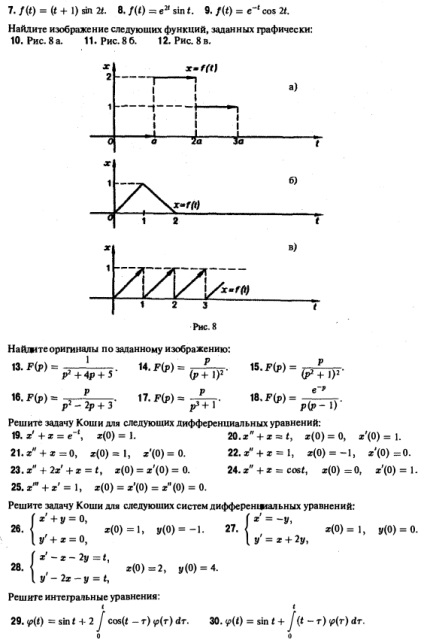
Korábban megnéztük a Fourier transzformációs integrál a kernel K (t, Q = f Fourier-transzformáció kényelmetlen, hogy legyen a feltétele a teljes integrálhatóság az f (t) a teljes tengely t, Laplace-transzformáció segítségével, hogy kitörjön a korlátozás. Definíció 1. Funktsiey- majd nazyvatvsyakuyu eredeti komplex értékű függvény f (t) deystvitsl Nogo argumentum t, yushuyu kielégíti az alábbi feltételeket: 1. f (t) folytonos az egész T tengely, eltekintve az egyes pontokat, ahol f (t) a 1. rendű diszkontinuitás, ahol nakazhdom véget intervaleosi * t kihtochek mozhetbyt csak véges számú, 2. az f (t) zérus negatív értékei t, F (t) = 0 t 3 növekvő F modul (t) nem növeli gyorsabb exponenciális függvény, azaz, vannak M szám .. > 0 és s úgy, hogy minden t világos, hogy ha a egyenlőtlenség (1) tartja bizonyos s = aj, akkor kell végrehajtani, és minden 82> 8]. infima s0 összes számát „a = INF, amelyre a egyenlőtlenség (1) az úgynevezett növekedési indikátor függvény f (t). Megjegyzés. Általában az egyenlőtlenséget nem rendelkezik, de a becslés, ha e> 0 - bármikor. Ez a függvény a növekedési ráta = B0 Számára egyenlőtlenség \ t \ ^ M V * ^ 0 nem rendelkezik, de a egyenlőtlenség | f | * Mei. Állapot (1) sokkal kevésbé szigorú, mint a feltétel (*). 1. példa a funkció nem felel meg a feltétel ( „), de a feltétel (1) teljesül bármely s ^ I és A / ^ I; növekedési üteme 5 ° = • • Tehát mi a funkciója eredeti. Másrészt, a funkció nem működik, az eredeti: van végtelen érdekében növekedés, „a = + oo. A legegyszerűbb funkció, az eredeti egy úgynevezett unit funkció Ha a funkciója megfelel a feltételeknek az 1. és 3. Definíció 1, de nem felel meg a 2. feltétel, a termék már olyan funkció-eredeti. Az egyszerűség kedvéért, akkor, mint egy szabály, rj (t) tényező csökken, feltéve, hogy az összes funkcióját, hogy úgy véljük, nullával egyenlő negatív t, mivel, hogy amikor bizonyos f (t), például mintegy sin Ty cos t, El, stb ez mindig értjük a következő tulajdonságokkal (2. ábra).: .. n = n (0 1. ábra 2. Definíció Legyen f p.) = e