Ládák és érmék elemzése Kis adatok

Tehát, válaszolva az eredeti probléma, persze, 2/3, bár a többség az internet felelős 1/2. Amikor először válassza ki az egyik 6 pénzérmék, amelyek a ládákat. Az esetek felében lesz arany - azaz három esetben (válassza a második aranyat a mellkas vagy az első vagy a második aranyat a harmadik)! A két ilyen három esetben válasszon az ugyanazon törzsön érme arany. Tehát a válasz: 2/3.
Emlékeztet Monty Hall. nem igaz? Most tekintsük általánosítások a probléma, amit kitalált magának (mint az internet nem szerepel).
Te N + 1 mellkasi, mindegyik N érméket. Összesen: N (N + 1) / 2 aranyat, az azonos mennyiségű ezüstöt. Ezek vannak elosztva a ládák a következők (lásd ábra esetében N = 5 ..):
Úgy döntünk, egy ilyen láda véletlenszerűen, és vakon húzza ki az egyik érmét. Ez az arany. Mi a valószínűsége, hogy a második érme, kivont vakon ebből törzse is, az arany?

Meglepő módon a válasz független a N! Mindig 2/3!
Sőt, mi extraháljuk arany érme - az egyik N (N + 1) / 2. Lehet, hogy nem az első csomagtartóban. Ha ez a második - esélye, hogy nyomokban aranyat nulla. Ha ez a harmadik, az esélye nyomainak eltávolítása arany - 1 / (N-1), stb Azt látjuk, hogy a szükséges valószínűség értéke
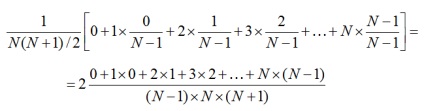
Továbbra is azt mutatják, hogy a nevező a számlálóban osztva 3, amely könnyen elvégezhető indukciós.
Személy szerint én ezt a tényt (hogy a válasz mindig 2/3) csodálkozva szórakozott. Valahogy úgy tűnt, hogy a növekvő N, annak a valószínűsége kell törekednünk, hogy 1/2. Vagy valahogy változtatni, mert az eredeti probléma az volt, hogy pontosan 3 fiókos 2 érmét, így a válasz áll a 2. és 3. „nem fáj a szeme”, és miért van az N-dimenziós eset. De még ennél is én intuíció elvezetett ez az általánosítás:
Te N + 1 mellkasi, mindegyik N érméket. Összesen: N (N + 1) / 2 aranyat, az azonos mennyiségű ezüstöt. Ezek vannak elosztva a ládák a következők (lásd ábra esetében N = 5 ..):
Úgy döntünk, egy ilyen láda véletlenszerűen, és vakon húzza ki érmék K (K Alexey Shramkov. Jó napot kívánok. P (A | B) = P (AB) \ P (B) Egy adott állapot a probléma az egyértelműség, csupán egy vak választás. Ez az elrendezés a klasszikus probléma a célt. Ha teszünk egy lövés. És meghatározza a valószínűsége, ütő a 10, ha tudjuk, hogy még elérje a célt. Esélye, hogy elérje valahol a 60% -os célkitűzés és a valószínűsége, ütő 10 - 30%. Azt írják egyéb feladatokat. Sőt, te magad is írt, és hogyan: Mi a valószínűsége annak, hogy egy láda aranyat 2, feltéve, hogy van egy aranyat. Ez a valószínűség - 1/2. De van egy kérdés: mi a valószínűsége, hogy a rajz egy második aranyérme után az első arany. Ie nem olyan hosszú, mint tudjuk, hogy van egy arany (néznénk a csomagtartóban), és feltéve, hogy az általunk előhúzott egy arany érme, és ez a kezében (ez egy vak választás: tudjuk, hogy már volt egy arany érme, és semmit sem tud a második). Ezért kell emlékezni, hogy az utolsó mellkasi és húzza ki az első arany a valószínűsége, mint a második. P (2 szol | sol 1) = F (mindkettő sol) / P (sol 1) P (2 szol | sol 1) = F (mindkettő sol) / P (sol 1) = (1/3) / (1/2) = 2/3 Alexey Shramkov. Alexander, kösz a pontosítást - Teljes mértékben egyetértek az eredmény a finomítás, hogy „mi a valószínűsége, hogy a rajz egy második aranyérme után az első arany”, azaz ebben az esetben tudjuk kihúzni a második érme másik mellkasát. A készítmény a probléma összezavart az, hogy nem tudjuk megváltoztatni a választás a mellkas az első vak választás, de egyszerűen húzza ki a többi a második érme. „Mi a valószínűsége, hogy a második érme a csomagtartóban - azonos arany?” Nem, várj egy percet. Úgy van, ahogy meg van írva, hogy mi a valószínűsége, hogy a rajz egy második aranyérme ugyanazon törzsön (én tényleg azt jelentette, alapértelmezés szerint - feleslegesen szerepel feltétel). Az eredeti megfogalmazás helyes - nem változtatunk a mellkasát.
Hol vagyok rosszul érvelés? A válasz 50% helyesnek tűnik a nyers adatokat.
B-esemény, amelynek kiválasztása után a csomagtér> = 1 aranyat benne
P (B) = 2/3.
A-esemény, amely kiválasztása után a mellkas = 2 aranyat abban
P (A) = 1/3
A probléma az, hogy megtalálják a valószínűsége egy esemény az A, B, miután az esemény bekövetkezett, azaz a
P (A | B) -?
A és B-függő események.
Annak a valószínűsége, együttes előfordulása két függő események a termék a valószínűsége egyikük a feltételes valószínűsége, hogy a második, számított a feltétellel, hogy az első esemény történt, azaz,
P (AB) = P (B) * P (A | B) => P (A | B) = P (AB) / P (B), ahol P (AB) = P (A), szükségtelenül esemény a befektetett esetén B.
P (sol 1) = P (1 szol | 2. mellkas) R (2d törzs) + F (1 szol | harmadik törzs) P (harmadik törzs) = 0,5 * 1/3 + 1 * 1/3 = 1/2Kapcsolódó cikkek