Laboratóriumi munka №10
Gráfelmélet nemrég széles körben használják különböző területeken a tudomány és a technológia. A gyors fejlődés az elmélet kapott a létrehozását számítógépes technológiát, amely lehetővé megoldani sok algoritmikus feladat.
Count - kombinációja a két véges halmazok: egy sor pontot és egy sor összekötő vonalak néhány pár ilyen pont. A pontok halmaza nevű csúcsot (csomópontok) a grafikon. Sokaságát összekötő vezetékek a gráf, az úgynevezett a szélek (ívek) a grafikon.
Irányított gráf (digráf) - egy grafikon, amelyben az összes éleket orientált, vagyis, amelynek az élei vannak hozzárendelve az irányt.
Irányítatlan gráf (neorgraf) - gráf minden éle egy irányítatlan, azaz amelynek szélei nem definiált irányba.
Vegyes Count - Count egyaránt tartalmazó irányított és irányítatlan élek.
A hurok egy él. összekötő vertex önmagával. Két csúcsot nevezik szomszédos, ha van él összekötő őket. Bordákkal. összekötő azonos pontpár nevezzük többszörösei.
Egyszerű gráf - egy grafikon, amely nem hurkok vagy többszörös élek.
Multigráf - egy grafikon, amelyben bármely két pont között több, mint egy szélét.
Útvonal a gráf egy véges váltakozó sorrendben a szomszédos csúcsok és az élek csúcsokat összekötő.
Az útvonal nyitott, ha annak kezdete és vége csúcsok különböző, egyébként azt mondják, hogy le kell zárni.
Az útvonal nevezzük egy lánc. ha minden széle különbözőek. A nyitott áramkör nevezzük utat. ha minden csúcsot különböző.
A zártláncú nevezzük ciklust. ha minden csúcsa különböző, kivéve a végén.
A gráf összefüggő, ha van egy módja az őket összekötő bármely két csúcsa van.
vertex tömeg - szám (valós, egész vagy racionális) szolgáltatott levelezést a felső (értelmezni költség, teljesítmény, stb ...). Súly (hossza) a borda - szám vagy egy pár számot, amely értelmezi a hosszához képest az él, a sávszélesség, stb ...
Súlyozott gráf - grafikon, minden él van rendelve egy bizonyos értéket (az él súlyát).
Válogatás a adatszerkezetet tároló a számítógép memóriájában a grafikon alapvető fontosságú a fejlesztés hatékony algoritmusok. Vegyünk egy pár módon, hogy képviselje a grafikonon.
Mivel egy grafikont a csomópontok száma n, és az élek számát - m. Mindegyik borda csúcshoz, és minden van egy tömeg - egy pozitív egész szám. Ha a gráf nem jelzett, úgy véljük, hogy a súly egyenlő eggyel.
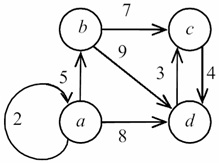
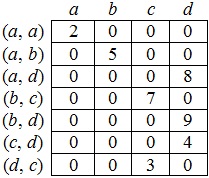
Listája bordák - ez meg van kialakítva pár szomszédos csúcsok. A tárolási tipikusan egy egydimenziós tömb hossza m, tartalmaz egy listát pár csúcsok szomszédos egyik széle a grafikon. Listája bordák sokkal kényelmesebb, hogy végre különböző algoritmusok grafikonon, mint más módszerekkel.
A szomszédsági mátrix - egy kétdimenziós tömböt n dimenziós X n, elemek értékeit, amelyekre jellemző smezhnostyuvershin grafikon. Ebben az esetben az értéket a mátrix elem van hozzárendelve az élek számát, amelyek összekötik a megfelelő csúcsokat. Ez a módszer hatékony, ha ellenőrizni kell a szomszédsági vagy talál tömeg szélén a két adott csúcsot.
Mátrix esetén - egy kétdimenziós tömb dimenzió n x m, amely meghatározza a kapcsolat a beeső grafikon elemek (EDGE és vertex). Az oszlopok a széleket. vonal - magasságokba. Egy nem nulla értéket a cellába a mátrix jelzi a kapcsolatot a felső és szélét. Ez a módszer a legtöbb tágas tároló, de megkönnyíti, hogy megtalálja ciklusban a grafikonon.
Sok gráfalgoritmusok, amelyek alapján a szisztematikus számbavételét csúcsok. oly módon, hogy minden csúcs megtekinthető (látogatott) pontosan egyszer. Ezért fontos feladat az, hogy megtaláljuk a jó módszereket keresni a dobozban.
Megoldásában sok probléma, a grafikonok, szükségünk van hatékony módszerek rendszeres kiszállítási csúcsok és az élek. A standard és a leggyakoribb módszerek a következők:
Ezek az eljárások leggyakrabban tekintik irányított gráf. de ők is alkalmazható a külföldi-orientált, élek minősülnek kétirányú. bejárás algoritmusok mélysége és szélessége a döntése alapján a különböző grafikonok feldolgozási feladatok, mint például építésére átívelő erdőben. proverkisvyaznosti. acyclia, számológépek közötti távolságok csúcsok és mások.