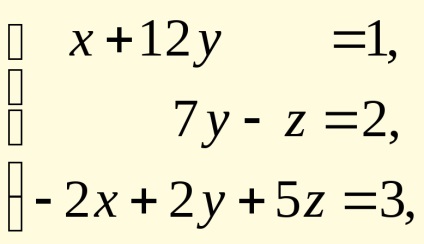Lab Mathcad 3_6
Laboratóriumi munka № 4
Differenciálása funkciókat. Geometriai értelmében a származék.
Cél. Ismerje meg, hogy megtalálják a számértéke differenciálhányados egy adott ponton.
Kiszámítása a származék egy függvény.
Mathcad származékot üzemeltető megtalálásához számértéke differenciálhányados egy adott pontban. Kiszámításához származtatott kulcs van, hogy aláírja? .
Annak érdekében, hogy megtalálják a függvény deriváltját, és számítsuk ki számérték, akkor a következőket kell tennie:
Először is, meg a pont, ahol meg akarja találni a származék.
Kattints az alábbi meghatározásokat ebben a kérdésben. Majd tárcsázza. Ez lesz az üzemeltető a származtatott két területen:
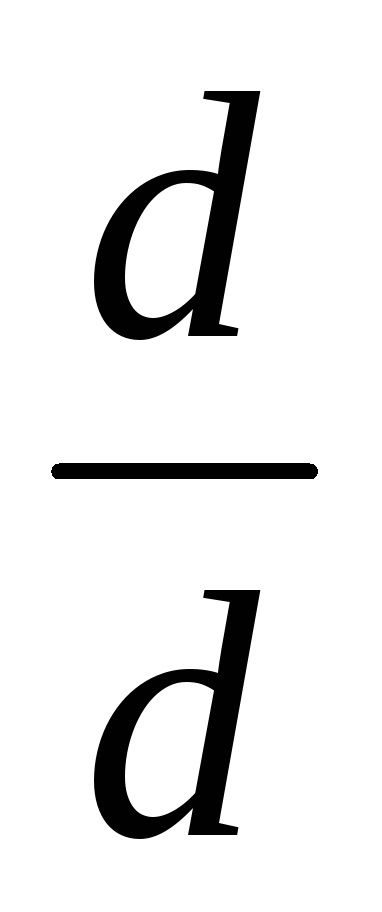
Kattintson a pályán a nevező, és írja be a változó nevét, amelyen a differenciálás végzik.
Kattintson a mező jobb oldalán
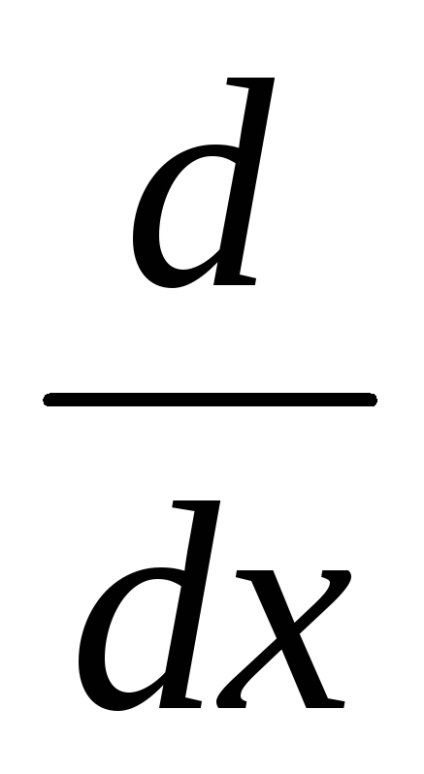
Az eredmény megtekintéséhez nyomja meg a = jel.
1.1 Feladat Keresse származék ponton
Mi az a pont, ahol meg akarja találni a származék:
Bemutatjuk a származékos kezelő, a mezők és kiszámítja a származékos:
* Az eredmény a differenciálódás nem függvény, és a számát - az érték a származék egy adott ponton a differenciálódás változó.
Bár differenciálódás vissza csak egy szám, akkor meg egy függvényt egy másik funkciója, mint a származék. Például:
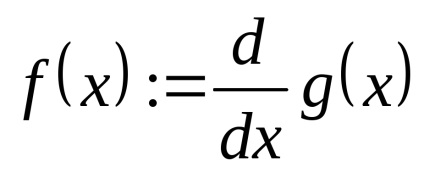
Kiszámítása f (x) visszatér egy numerikus derivált formában, g (x) az x.
Expression meg kell különböztetni, lehet valós vagy komplex.
Változó differenciálás legyen egyszerű, nem indexelt változó.
Geometriai értelmében a származék.
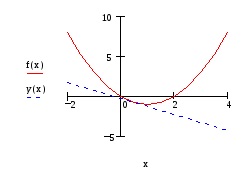
Feladat 1.2. Dana funkció = f (x). Ábrázoljuk a tangens függvény és a grafikon a ponton az abszcissza x = x0, ha - az egyenlet az érintő.
Bemutatjuk a funkciót, és megtalálja a megfelelő érték a lényeg:
Keressük a származékot ezt a funkciót a ponton:
Az egyenlet az érintési ezt a funkciót:
Építünk a függvény grafikonját és érinti azt.
Célok 3. Végezze eltérés számítások szimbolikus formában:
Feladat 4. Keresse meg a függvény deriváltját bármely pontján.
Cél. Ismerje meg, hogy megtalálják a határozott integrálok funkciók számítani a területet egy alak segítségével integrál.
integráló operátor Mathcad numerikus számítás egy határozott integrál függvény felett bizonyos intervallum.
A szerves jel jelenik meg, ha megnyomja a gombot, a jel .
Annak érdekében, hogy kiszámítja a határozott integrál, akkor a következőket kell tennie:
Kattintson az üres területre, és írja jel . Látni fogja a szerves jele üres mező az integrandus, korlátait az integráció és a változó integráció: ∫
Kattintson a doboz alján és pontszám alsó határa az integráció. Kattints a felső mező típusától és a felső határ az integráció.
Kattintson a mező közötti szerves megjelölés és a d és írja a kifejezést, hogy integrálni kívánt.
Kattintson az utolsó üres mezőt, és írja be a változó az integráció.
Az eredmény megtekintéséhez nyomja meg a = jel.
Bemutatjuk az integrál jel, és töltse ki a mezőket;
* A határértékek integrációs valósnak kell lennie. Expression integrálandó lehet valós vagy komplex. A további integráció változó, minden változó az integrandus kell előzőleg máshol meghatározott munkadokumentum. Változó integráció kell egy egyszerű változó nélküli index. Ha a változó az integráció egy dimenziós mennyiség, az alsó és felső határa az integráció kell az azonos méretű.
Szögletes formák. Mint ismeretes, útján határozott integrál számítható terület az ábra.
Építünk a grafikonok ezeket a funkciókat egy képet box:
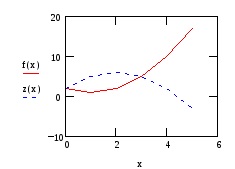
Mi területének kiszámítására a kapott szám:
Feladat 2.1. Fuss szerves számítás szimbolikus formában:
Feladatok 3.1 Számítsuk ki a határozott integrál.
Feladat 3.2. Keresse meg a területet az ábra által határolt grafikonok a funkciók. Ahhoz, hogy épít ez a szám.
Lineáris egyenletrendszer
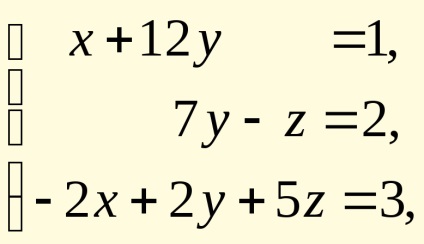
amelyben az arányok a négyzetes mátrix az ismeretlenek
, és a szabad tagok egy mátrixban, akkor
írva, mint a mátrix-egyenlettel, ahol van egy oszlop mátrixa az ismeretlenek. Az oszlop ismeretlen a mátrix-egyenlettel megszorozzuk a részek által hagyott a fordított mátrixba, amely csak, ha a meghatározója a rendszer eltér a nullától. Az eredmény (óta. Amennyiben az identitás mátrix). Ez a megoldási módja a lineáris egyenletrendszer az úgynevezett mátrix módszer. A mi esetünkben, megkapjuk (numerikus és szimbolikus)
Vizsgáljuk meg a megoldás abban rejlik, hogy ebben az esetben a megoldást találtak a mátrix egyenlet, amely ebben az esetben alkalmazni kell a valódi egyenlőség. Ennek eredményeként a helyettesítési kapjuk:
3.1. Keresse meghatározója a mátrix, és az inverz transzponáltja a mátrixban.
5x5 mátrix teszik ki a saját.
3.2. Oldjuk meg a lineáris egyenletrendszer segítségével a mátrix módszer.