Konvertálása derékszögű koordinátákat a síkban
Ha a teljes (5,17) görbét ad a másodrendű nem-degenerált, lehet csökkenteni, hogy kanonikus formában bevezetésével egy új rendszer a derékszögű koordináta-tengely nyilvánvaló forgatás egy meghatározott szöggel, és egy megfelelő transzfer indul.
A megszerzett eredetű (párhuzamos fordítás tengely) egy pont koordinátáit repülőgép az eredeti koordinátarendszerben (régi) és koordinátáit ugyanazon a ponton a transzformált rendszer (új) kapcsolatos a következő transzformációs képletek:
ahol - a koordinátáit egy új kezdet képest az eredeti rendszer (5.16 ábra).. A transzformációs képletek (5,22) csak akkor érvényesek, ha a tengelyek mindkét rendszer van kiválasztva az azonos méretű egység.
Ha az általános egyenlet másodrendű görbe (5.17) együttható a munkadarab koordinátarendszer nulla
(), A kezdeti koordinátarendszer párhuzamos tengely a szimmetriatengelye a görbe, és a vezetés az egyenlet a kanonikus formában csak akkor szükséges, hogy megfelelő, párhuzamos transzlációs tengely az új start. Ez megtehető elszigetelten négyzetek egyenlet, illetve ezt követően a származási egy pontot a transzformációs képletek (5,22).
Példa. Csökkentsd a egyenletet kanonikus formában és építmények által adott ez az egyenlet görbe.
◄ Ebben az egyenletben együtthatók. . Ezért, akkor adjon meg egy kört. Válassza az egyenletben a tökéletes négyzet :. Csere. Az egyenletek kanonikus formában. amely meghatároz egy síkot kör sugara. A központ ennek a körnek a kezdete egy új koordináta rendszerben. mint az eredeti rendszer, ez a központ található, a koordináták (ábra. 5.17). Kerülete a ponton érintő a tengelyen. Mi kerülete szerezni metszéspontjai tengelyével, forgalomba az eredeti egyenlet és megoldása a kapott másodfokú egyenlet. . ►
Ha az általános egyenlete a másodrendű görbe (5.17) együttható nem nulla, a koordináta-tengelyek nem párhuzamosak a szimmetriatengelye a másodrendű görbe. Annak érdekében, hogy ezek a tengelyek párhuzamosak, forgatni koordinátatengelyeken szögben. amely egyenlő az eredeti közötti szög a koordináta-rendszer tengely és egy pozitív irányba az egyes szimmetriatengelye a görbe. Ez a szög határozza meg a képlet
Kanyarodáskor tengelyek (. Ábra 5.18), a koordinátákat a síkban a transzformált koordinátarendszer (új), és a koordinátái ugyanazon a ponton az eredeti rendszer (régi) kapcsolatos a következő transzformációs képletek:
Az inverz transzformáció:
Ha megadja a mátrixban. . . az átalakulás (5,24) felírható mátrix formában:
Az inverz transzformáció (5,25) mátrix formában a formája:
ahol - a fordított mátrixba.
Példa. Construct görbe által megadott egyenlet.
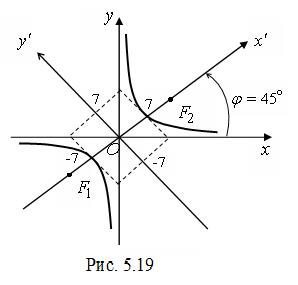
◄ Egy adott másodfokú egyenlet együtthatókat (cm. 5.17). . az összes többi nulla. Találunk invariáns görbe :. . . Ettől. . . arra a következtetésre jutunk, hogy ez az egyenlet határozza meg a hiperbola, a szimmetria tengelye, amely nem párhuzamos a koordináta tengelyeket és a vezetés az egyenlet a kanonikus szükséges forgástengelye. A szükséges forgásszög határozzuk meg képletű (5,23). Ettől. A nevező a képletben nulla, tehát. Amikor elforgatjuk a koordináta-tengelyek szögben átmenet régi az új koordinátákat kell megadni (5,25) a következő átváltási képlet:
Behelyettesítve az eredeti egyenlet a régi helyét az új, van: