Kiszámítása a nyomásveszteség a vízvezetékek, légcsatorna, folyómedrek

Egyedülálló felfedezés. VV Erokhin re Torez talált hosszirányú erő mágnesesség Több
Alapján képletek gyűjtött ebben a cikkben,
Ez történt a kis program kiszámítja a nyomásveszteség
a csövek a fűtési és a víz, a légcsatorna,
a folyómedrek és ereszcsatorna.
A számítás főleg a könyv
prof. A. V. Teplova hidraulika alapjai Leningrád Az energia 1965 ..
Letöltés programa Poteri_napora.xls 69 kB.
Az áramlás a víz, a levegő lamináris (azaz nyugodt, sima, vortex-mentes), és turbulens (örvénylő). Az alacsony áramlási sebességek lamináris mozgás. Nagy sebességgel - a turbulenciát. Mozgással szembeni ellenállást a csövekben alatt lamináris jellege sokkal alacsonyabb, mint a turbulens. (A légi közlekedésben a külső áramlását körül a szárnyak és a törzs a kép megfordul.). A határ az átmenet a lamináris áramlás turbulens áramlás határozza meg a kritikus Reynolds szám.
A folyadék és levegő képletű azonosak. Nem számít, mi a mérete az áramlás. a levegő áramlási járat egy csövön keresztül 5 mm átmérőjű, a levegő beáramlását a tartályba, és az áramlás a Volga kilométeres csatorna szélessége engedelmeskedik azonos törvényeket hidrodinamika.
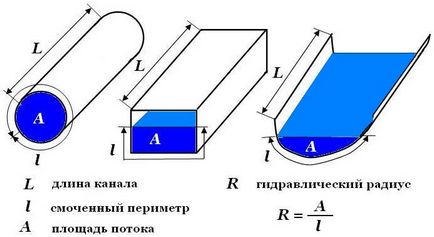
Egy tetszőleges alakja a csatornát, amelyet a mozgó patak, a Reynolds-szám:

v - Áramlási sebesség m / s
A - áramlási terület m 2,
l - m nedvesített kerület,
ν - kinematikus viszkozitása 2 m / s,
Levegő ν = 0,000 014 m 2 / s,
Víz ν = 0,000 001 m 2 / s,
RG - hidraulikus sugár az aránya az áramlási területének és nedves kerületének m.
A kritikus Reynolds-szám, amelynél a lamináris áramlás válik turbulens, jól 239.
Szögletes, teljesen kitöltve, cső Reynolds-száma:
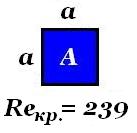
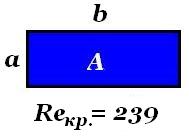 A téglalap alakú, teljesen kitöltve, csövek Reynolds-szám:
A téglalap alakú, teljesen kitöltve, csövek Reynolds-szám:

Kritikus, hogy hány négyzet és téglalap alakú csövek 239 is megegyezik.
 Kerek teljesen megtöltött cső Reynolds szám különbözik:
Kerek teljesen megtöltött cső Reynolds szám különbözik:

Kiszámításánál a Reynolds-szám kerek csövek gyakran nem szubsztituált hidraulikus sugár, az átmérője a cső, amely a 4-szer a hidraulikus sugár
A félreértések elkerülése végett meg kell tudni, hogy melyik jellemző dimenzió kiszámításához használt. Ha a hidraulikus sugara képletű kioldott, meg kell össze kell hasonlítani a kiszámított értéket Re 239, és ha kioldott átmérőjű, kör alakú cső, téglalap alakú cső oldalán vagy átlós, a kritikus szám 956.
Hozzá kell tenni, hogy a Reynolds szám inkább „homályos” jelző. A turbulencia folyamatok erősen befolyásolja a kezdeti jelenléte örvénydiffúzió áramlás, felületi érdesség, a test alakjához, hogy kölcsönhatásba lép az áramlás. Ezért ezek a kritikus Reynolds szám egyenlő 956 csőből megtöltött és 239 egyéb esetekben nem túl pontos. A szakirodalom értékeket, amelyek eltérnek a 2-szeres. Ezen kívül van egy széles közötti átmeneti tartományban a lamináris és turbulens áramlás nincs egyértelműen meghatározott határok, így zár az átmeneti ponton függ a személyiség a kísérletvezető.
A program kiszámításához nyomásveszteség kerek csövek podstvalyaetsya átmérőjű, és más esetekben, szemben a technika Teplova, négyszeres hidraulikus sugárral. Ez úgy történik, hogy a kritikus Reynolds-szám minden esetben fordult Odinokova és egyenlő 956.
Ellenállás mozgása a folyadék lamináris áramlás sebességével arányos az áramlás, és a turbulens áramlás négyzetével arányos a sebesség. A turbulens áramlási ellenállást csatornák növekvő sebesség növekedésével sokkal gyorsabb.
A nyomásesés egy kör alakú cső lamináris Poiseuille áramlás képlettel összhangban Re

Az áramlási sebesség és áramlási sebessége rokonságban
Professzor A. V. Teplov könyvében „alapjai hidraulika,” azt mondja, hogy a 19. század közepén azt javasolta, néhány száz tapasztalati képletek kiszámításához az áramlási ellenállást. A megadott képletek itt professzor fejlesztette A. Teplov kezeléssel a kísérleti adatok. A képletekben megszámoltuk Reynolds száma és az érdessége csatornák. Felelős hivatalos számítások kell kezelnie, ahogy az a vonatkozó állami előírásoknak, így ez a technika alkalmas közelítő számításokat.
 A nyomásesés egy kör alakú cső teljesen tele turbulens áramlást Re> Rekr.
A nyomásesés egy kör alakú cső teljesen tele turbulens áramlást Re> Rekr.
A nyomásesés a csővezetékbe, vagy egy tetszőleges alakú turbulens áramlást Re> Rekr.
érdességi értékek a δ prof. A. V. Teplovu
A függőség a dinamikus és a kinematikus viszkozitás a hőmérséklet és a nyomás.
Dinamikus és kinematikai vyazkozt kapcsolódó szorzó sűrűség:
Megadott paraméterek atmoszferikus nyomáson, hőmérsékleten 0 Celsius fok.
Ahol t - a hőmérséklet Celsius-fokban.
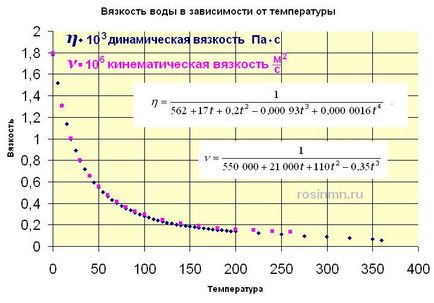
A telek a dinamikus és kinematikus viszkozitása a víz hőmérséklete
A víz sűrűsége csökken a hőmérséklet növekedésével a törvény szerint
A dinamikus viszkozitás a levegő nagymértékben függ a hőmérséklet és a nyomás. Amikor a nyomás növeli a levegő sűrűsége, kinematikus vyazkozt ezért hányadosaként kapott dinamikus vyazkozti a sűrűség jelentősen csökken a hőmérséklet növekedésével.
A könyv Nyesztyerenko AV alapjai termodinamikai számítások szellőztető és légkondicionáló IMS 1971 dinamikai viszkozitás a képlet a levegő
On www.dpva.info helyszínen egy olyan táblázat paraméterektől függően a levegő nyomása és hőmérséklete. Graph Dinamikus viszkozitás szerint épült ez a táblázat.
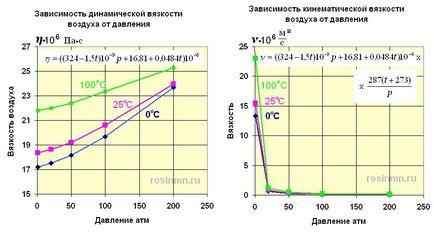
A telek a dinamikus és kinematikus viszkozitása levegő nyomás és hőmérséklet
Ez a grafikon nagyon pontosan közelítéssel lineáris egyenletek. A hiba nem haladhatja meg a 2%.
Annak érdekében, hogy kiszámítja a kinematikai viszkozitás szükséges ismerni a levegő sűrűsége. A gáz sűrűségét számítjuk ki az ismert Clapeyron törvény:

Az áramlási sebesség és áramlási sebessége rokonságban
Professzor A. V. Teplov könyvében „alapjai hidraulika,” azt mondja, hogy a 19. század közepén azt javasolta, néhány száz tapasztalati képletek kiszámításához az áramlási ellenállást. A megadott képletek itt professzor fejlesztette A. Teplov kezeléssel a kísérleti adatok. A képletekben megszámoltuk Reynolds száma és az érdessége csatornák. Felelős hivatalos számítások kell kezelnie, ahogy az a vonatkozó állami előírásoknak, így ez a technika alkalmas közelítő számításokat.
 A nyomásesés egy kör alakú cső teljesen tele turbulens áramlást Re> Rekr.
A nyomásesés egy kör alakú cső teljesen tele turbulens áramlást Re> Rekr.

A nyomásesés a csővezetékbe, vagy egy tetszőleges alakú turbulens áramlást Re> Rekr.

érdességi értékek a δ prof. A. V. Teplovu
A függőség a dinamikus és a kinematikus viszkozitás a hőmérséklet és a nyomás.
Dinamikus és kinematikai vyazkozt kapcsolódó szorzó sűrűség:
Megadott paraméterek atmoszferikus nyomáson, hőmérsékleten 0 Celsius fok.
Ahol t - a hőmérséklet Celsius-fokban.

A telek a dinamikus és kinematikus viszkozitása a víz hőmérséklete
A víz sűrűsége csökken a hőmérséklet növekedésével a törvény szerint
A dinamikus viszkozitás a levegő nagymértékben függ a hőmérséklet és a nyomás. Amikor a nyomás növeli a levegő sűrűsége, kinematikus vyazkozt ezért hányadosaként kapott dinamikus vyazkozti a sűrűség jelentősen csökken a hőmérséklet növekedésével.
A könyv Nyesztyerenko AV alapjai termodinamikai számítások szellőztető és légkondicionáló IMS 1971 dinamikai viszkozitás a képlet a levegő
On www.dpva.info helyszínen egy olyan táblázat paraméterektől függően a levegő nyomása és hőmérséklete. Graph Dinamikus viszkozitás szerint épült ez a táblázat.

A telek a dinamikus és kinematikus viszkozitása levegő nyomás és hőmérséklet
Ez a grafikon nagyon pontosan közelítéssel lineáris egyenletek. A hiba nem haladhatja meg a 2%.
Annak érdekében, hogy kiszámítja a kinematikai viszkozitás szükséges ismerni a levegő sűrűsége. A gáz sűrűségét számítjuk ki az ismert Clapeyron törvény: