Kiszámítása a jelen (a jelen, áram) érték MS Excel - kompatibilis a Microsoft Excel 2018
RasschitaemPrivedennuyu (az aktuális idő) stoimostinvestitsii különböző módszerek alapján százalékban: általános képletű egyszerű százaléka, összetételéhez, és abban az esetben a járadék kifizetések tetszőleges értéket.
Jelenérték (jelenérték) számítása alapján a koncepció az idő pénz értéke: pénz áll most, többet ér, mint az azonos mennyiségű a jövőben, mivel a bennük rejlő jövedelmet. A számítás a jelenérték, valamint a jövőbeli érték azért fontos, mert kifizetések különböző időpontokban lehet hasonlítani csak azok csökkentésének egyetlen időpontban.
A jelenérték eredményeként kapott működtetési jövőbeli bevételek és ráfordítások a kezdeti időszak, és attól függ, milyen módszerrel a kamatozó: egyszerű érdeklődés. vegyület érdeklődés vagy járadék (az adott példában például tartalmazó oldatot az egyes módszerek).
egyszerű kamat
A módszer lényege az egyszerű kamatszámítás az, hogy a felhalmozódott kamatot élettartama alatt a beruházás az azonos mennyiségű (felhalmozott kamatot a korábbi időszakokban nem kerülnek aktiválásra, azaz ezek érdeklődés a későbbi időszakokban nem kell fizetnie).
MS Excel, hogy olvassa el a jelen értéket a rövidítése PS (PS jelenik meg, mint egy érv sok MS EXCEL pénzügy funkciók).
Megjegyzés. MS Excel nincs külön funkció kiszámításához a jelen értéke a módszer egyszerű érdeklődés. PS () funkció kiszámításához használt százalék esetében komplex és életjáradék. Míg meghatározva az argumentum NPER értéke 1, és mint ráták jelzik i * n, akkor lehet, hogy a SS () kiszámításához a jelen érték, és a módszer egyszerű kamat (lásd. A példa fájl).
Ahhoz, hogy meghatározzuk a jelen érték kiszámításakor százaléka használata egyszerű kiszámításának képlete a jövőbeli érték (FV):
FV = PV * (1 + i * n)
ahol PV - jelenértéke (az összeg, amelyet a befektetett a pillanatban, és amely a felhalmozott kamatot);
i - a kamatláb a kamatozási időszakra (például, ha a kamat kiszámítása évente egyszer, az éves, ha kamatfizetési kötelezettség terheli havi, hó);
N - száma időtartamok, amely alatt kamatozik.
Ebből a képletből kapjuk, hogy:
Így a számítási eljárást a jelen értékének kiszámítása a jövőbeli érték az ellenkező. Más szóval, melynek segítségével megtudhatjuk, hogy mennyit kell befektetni most annak érdekében, hogy egy bizonyos összeget a jövőben.
Például, szeretnénk tudni, hogy mennyi van ma szükség, hogy nyissa ki a betét, hogy felhalmozódnak 3 év 100 $ 000r. Tegyük fel, hogy egy bank működik aránya betétek 15%, és a százalékos számítjuk mind betét összege (egyszerű kamat).
Ahhoz, hogy megtalálja a válasz erre a kérdésre, meg kell számítani a jelen jövőbeli értéket összeget, amelyet a képlet PV = FV / (1 + i * n) = 100000 / (1 + 0,15 * 3) = 68 965,52r. Van, hogy a mai napon (a tényleges, valódi) összege 68 965,52r. az egyenértékű 3 év az összeg 100 000,00 dörzsölje. (A jelenlegi aránya 15%, és a számítási módszerét az egyszerű érdeklődés).
Természetesen a módszer a jelen érték nem veszi figyelembe az infláció, a csőd a bank, és így tovább. Ez a módszer működik hatékonyan összehasonlítására összege „ceteris paribus”. Például, hogy vele lehet megválaszolni a kérdést: „Mi az ajánlatot a bank jobban megéri venni, hogy 3 éven keresztül maximális összege: a betét egyszerű kamat 15% vagy kamatos havi kapitalizációja az arány 12% évente?” A választ erre a kérdésre, mi a jelenérték számítása során kamatos kamatot.
kamatos kamat
Ha a komplex kamatok kamat felhalmozott pénz után töltési idő, csatlakozzon az adósság. Így, a bázis a kompaundálási eltérően egyszerű százalékos változások az egyes számítási időszak. Csatlakozás a felhalmozódott kamat összegét, amely alapjául szolgált kiszámítására, az úgynevezett kapitalizációja az érdeklődés. Néha ez a módszer az úgynevezett „kamat érdek”.
Jelenértéke PV (vagy MS) kiszámítható a jelen esetben, a következő képlet segítségével elegyítési nehéz százalék.
FV = PV * (1 + i) ^ n
ahol FV (vagy S) - jövőbeni (vagy visszatöltött összeg),
i - az éves kamatláb,
n - kölcsön ideje években
Amikor kihasználva m-szor egy évben a jelen értéke képlet a következő:
PV = FV / (1 + i / m) ^ (n * m)
i / m - az a sebesség közötti időszakra.
Például, az összeg 100 000 dörzsölje. A elszámolási számla a 3. év megegyezik a jelenlegi összesen 69 892,49r. ha a jelenlegi érdeklődés aránya 12% (felhalmozódó% havonta; feltöltését nincs jelen). A kapott eredmény egy képlet = 100000 / (1% + 12/12) ^ (3 * 12), vagy az általános képletű SS = (12% / 12 3 * 12 0; -100000).
Egy kérdésre válaszolva az előző részben, „Mi a bank jövedelmezőbb hogy elfogadja az ajánlatot, hogy 3 éven keresztül maximális összege: a betét egyszerű kamat 15% vagy kamatos havi kapitalizációja az arány 12% évente?” meg kell összehasonlítani a két jelenérték: 69 892,49r. (Kamatos) és 68 965,52r. (Egyszerű kamat). mert A jelenérték, megfelelően kiszámított javaslata alapján a bank a betét egyszerű érdeklődés, kevésbé jövedelmező javaslatára (most kell befektetni kevesebb pénzt 3 év, hogy az azonos mennyiségű 100 000,00 dörzsölje.)
Kamatos (több összegek)
Mi határozza meg a jelenlegi értéke több összegek, amelyek különböző időszakokban. Ez úgy valósítható meg, MS () funkció vagy egy alternatív képletű PV = FV / (1 + i) ^ n
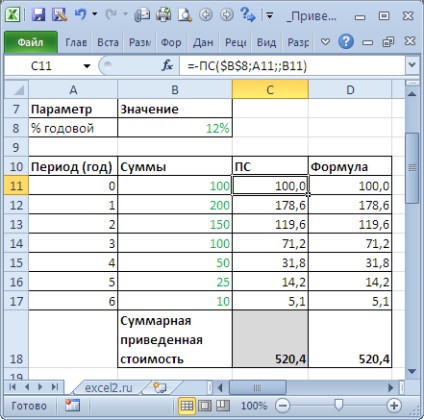
Azáltal, hogy az érték a kedvezmény mértéke 0%, megkapjuk az összeget a cash-flow (lásd. Példa fájl).
Ha amellett, hogy a kezdeti beruházás révén azonos időtartam készülnek több egyenlő kifizetések (kiegészítő beruházás), akkor a jelenérték lesz sokkal bonyolultabb (lásd. Cikk járadék. Határozzuk meg az MS Excel, hogy a (jelenlegi) értéke. Ami egy számítást a PV function () . és a kimeneti alternatív képletek).
Vannak más problémák elemzésére (lásd például a fájl.)
Jelenértékének meghatározására kifizetések esetén bármilyen nagyságrendű
kapcsolódó cikkek
Olvassa el más cikkeket, amelyek megoldják a hasonló problémákat MS Excel. Ez lehetővé teszi, hogy megoldja a széles osztálya hasonló problémákat.