Ismétlődő tizedes
Ne feledje, hogy a legelső lecke, beszéltem a tizedessel, hogy vannak számszerű frakciók, nem képviselheti egy tizedes (lásd. Lecke „tizedes törtek”)? Megtanultuk, hogy meghatározzák a nevezők a tényezőket, hogy vannak-e a számok más, mint 2 és 5.
Tehát hazudtam. És ma megtanuljuk, hogyan kell lefordítani a numerikus abszolút minden frakció egy tizedes. Ugyanakkor megismerjék az egész osztály frakciók végtelen értelmes részét.
Ismétlődő tizedes - bármilyen tizedes, amelynek során:
- Értelmes része áll egy végtelen számú számjegyet;
- Bizonyos időközönként a számok jelentős részét meg kell ismételni.
Egy sor ismétlődő számjegy alkotó értelmes része, az úgynevezett időszakos része a frakció, és a számjegyek száma a készletben - az időszak a frakció. A többi szegmens értelmes része, amely nem ismétlődik az úgynevezett nem periodikus része.
Mivel sok definíciók, meg kell vizsgálni részletesen néhány ilyen frakciói:
Ezt a frakciót találtak problémát gyakrabban. Nem periodikus rész: 0; periodikus rész 3; időszak hossza: 1.
Nem periodikus rész: 0,58; periodikus rész 3; időszak hossza: 1 újra.
Periodikus rész 1; időszakos része 54; időszak hossza: 2.
Nem periodikus rész: 0; periodikus rész: 641.025; időszak hossza: 6. Kényelmi szempontból ismétlő részek szóközzel elválasztva - a döntést, hogy erre nincs szükség.
Nem periodikus rész: 3066; időszakos 6. rész; időszak hossza: 1.
Mint látható, az időszakos frakció meghatározását koncepciója alapján significand. Ezért, ha elfelejtette, amit célszerű megismételni - lásd leckét „szorzás és az osztás a tizedes.”.
Az átmenet a periodikus tizedes
Tekintsünk egy közös frakció formájában a / b. Kibontásához nevező törzstényezős. Két lehetőség van:
- A bővítés már csak 2 multiplikátor és 5. Ezek a frakciók könnyen tizedes - lásd leckét „tizedes törtek.”. Ezek nem érint bennünket;
- Az expanzió van valami más mellett a 2. és 5. Ebben az esetben a frakció nem ábrázolható, mint decimális, de azt tudjuk, hogy egy ismétlődő tizedes.
Beállításához ismétlődő tizedes, meg kell találni a periodikus és aperiodikus része. Hogyan? Tegye a tekercs a rossz, majd ossza el a számlálót a nevező „terület”.
Ez kerül sor az alábbiak szerint:
- Először szét az egész részt. ha van;
- Lehet több szám a tizedesvessző után;
- Egy idő után, a számok kezdenek ismételni.
Ez az! Ismételt számokat tizedesvessző után jelöli a rendszeres része, de mi áll előtte - nem periodikus.
Feladat. Viszont rendes frakciókat periodikus decimális:
A frakciókat nélkül az egész részét, így csak osztani a számlálóban a nevező „sarok”:
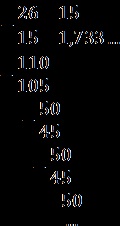
Mint látható, a maradék ismétlődnek. Írunk a frakció a „megfelelő” módon: 1733. = 1,7 (3).
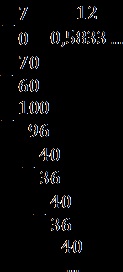
Az eredmény egy olyan frakció: 0,5833. = 0,58 (3).
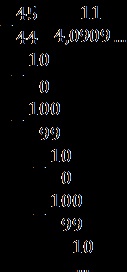
Írja be a szokásos módon: 4,0909. = 4 (09).
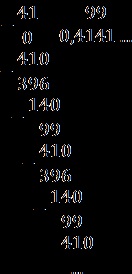
Mi lelövik: 0,4141. = 0, (41).
Átmenet a periodikus tizedes tört egy közönséges
Tekintsük ismétlődő tizedes X = abc (1 b 1 c 1). Szükséges, hogy lefordítja klasszikus „kétszintes”. Ehhez hajtsa végre négy egyszerű lépésből áll:
- Keressen egy frakció időszak alatt, azaz Hány szám van az időszakos része. Legyen száma k;
- Keresse meg a kifejezés értéke X · 10 k. Ez egyenértékű elmozdulás a tizedesvessző jobbra a teljes időszakban - lásd leckét „szorzás és az osztás jegyig” ;.
- Ebből számot kell levonni a kezdeti kifejezés. Amikor ez a periodikus része a „égett”, és általában összezúzzák;
- Az így kapott egyenlet, hogy megtalálják a X. Minden tizedessel lefordítani törzsrészvény.
Feladat. Hozd a közös áltörtek a:
Dolgozunk az első frakció: X = 9, (6) = 9,666.
csak egy szám szerepel zárójelben, így az időszak a k = 1. Ekkor megszorozzuk ezt a frakciót 10 k = január 10 = 10. Van:
10 · 10 X = 9,6666. = 96,666.
Vonjuk ki a kezdeti lövés, és oldja meg a következő egyenletet:
10 X - X = 96.666. - 9,666. = 96-9 = 87;
9 X = 87;
X = 87/9 = 29/3.
Most mi kell érteni a második frakció. Így, az X = 32 (39) = 32,393939.
Időszak k = 2, úgy, megszorozzuk az összes 10 k = 10 2 = 100:
X = 100 · 100 32,393939. = 3239,3939.
Ismét kivonni a kezdeti lövés, és oldja meg a következő egyenletet:
100 X - X = 3239,3939. - 32,3939. = 3239-32 = 3207;
99 X = 3207;
X = 3207/99 = 1069-1033.
Kezdve a harmadik frakcióban: X = 0,30 (5) = 0,30555. A rendszer ugyanaz, úgyhogy csak hogy a számítások:
Időszak k = 1 ⇒ megszorozzuk az összes 10 K 10 = 1 = 10;
10 · 10 X = 0,30555. = 3,05555.
10 X - X = 3,0555. - 0,305555. = 2,75 = 4,11;
9 X = 11/4;
X = (11/4). 9 = 11/36.
Végül, az utolsó frakció: X = 0, (2475) = 0,2475 2475. Ismét, a kényelem kedvéért időszakos alkatrészek vannak elválasztva egymástói hornyokkal. Van:
k = 4 ⇒ 10 k = 10 4 = 10000;
Az X 10000 = 10000 2475 · 0,2475 = 2475,2475.
10 000 X - X = 2475,2475. - 0,2475 = 2475. 2475;
X = 2475-9999;
X = 2475. 9999 = 25/101.
- frakciók összehasonlítása
- Teszt a leckét „tizedes törtek” (2. lehetőség)
- Kombinatorika a probléma B6: egyszerű teszt
- Mi a numerikus frakció
- sík egyenlet C2 feladat. 1. rész: mátrix és determinánsok
- Webinar a feladatok C1: Trigonometry
- Ingyenes Felkészülés a vizsgára 7 egyszerű, de nagyon hasznos tanulságokat + házi feladat
