Időközönként egyhangúságát funkció pont optimumfeltételekbe monotónia

Intervalymonotonnosti funkciót. Szélsőérték pont.

monotónia állapotban. Ha egy differenciálható függvény növeli az intervallum, akkor. Ha egy differenciálható függvény csökken az intervallum, akkor.

A lényeg pont az függvény minimuma, ha van olyan, hogy valamennyi, az intervallumot, és az egyenlőtlenséget.

A lényeg az úgynevezett maximális pontja funkció, ha van olyan, hogy valamennyi, az intervallumot, és az egyenlőtlenséget.

minimális és maximális pontot nevezzük pontok extrém funkciókat.

Kritikus pont az a pont, ahol a származék jelentése nulla vagy nem létezik.

Elégséges feltételei extrémuma.

1. Ha átmegy a kritikus pontot az első derivált előjelet, és a függvény folytonos egy pont, a pont funkció egy extrém. Továbbá, ha a jel változik a „+” „-”, akkor - a maximális pontot; ha az előjel változik a „-” „+”, akkor - a minimális pontot.

2. Ha a kritikus pont a második derivált nem nulla, és folyamatos a ponton, a pont funkció van egy szélsőérték. Továbbá, ha a pont a második derivált pozitív, akkor - a minimális pont; ha azon a ponton, a második derivált negatív, - a maximális pont.

Intervalyvognutosti és konvexitás a grafikon funkciók.

Graph konvex művelet akkor indul el, ha a tangens, hogy a görbe bármely pontján fekvő fölött ez a görbe (9. ábra).

A grafikon a konkáv, ha a tangens

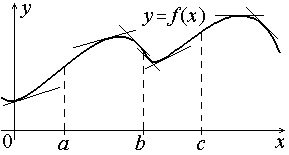
hogy a görbe bármely pontján alatt van ez a görbe (9. ábra).

Elégséges feltétele convexity. Ha a funkció kétszer differenciálható, és minden, a grafikon konvex.

Elégséges feltétele konkáv. Ha a funkció kétszer differenciálható, és minden, a grafikon konkáv.

Az a pont, amely megváltoztatja a konkáv voltának a grafikon egy ütközőnek vagy dudor a homorú úgynevezett inflexiós pontban.

Az inflexiós pont egy funkciója a pont, amelynél a függvény folytonos, és

A második derivált nullával egyenlő, vagy nem létezik;

amikor áthalad a pont a jele a második derivált.

Funkció két változó

A függvény két változó és készlet, ha minden számpár és egy bizonyos régióban egy bizonyos törvény kap értéket. A változók és függetlenek, és - függő változó (funkció).

A domain a funkció a pontok halmaza, ahol a funkció határozza meg.

A szám alapján az úgynevezett korlátozó funkció egy pontot, ha bármilyen létezik egy olyan, hogy ha a két pont közötti távolság vagy kevesebb, akkor:

A függvény deriváltját található a feltételezés, hogy állandó marad az úgynevezett parciális deriváltja, és jelöljük vagy:

A függvény deriváltját található a feltételezés, hogy állandó marad az úgynevezett parciális deriváltja, és jelöljük vagy:

Részleges 2. rendű függvény az úgynevezett részleges származékok elsőrendű parciális deriváltak:

- egy második parciális deriváltja;

- egy második parciális deriváltja;

- második kevert parciális deriváltja;

- második kevert parciális deriváltja.

A vegyes, részleges származékok egyenlő egymással, feltéve, hogy azok a folyamatos :.

A különbségek a függvény két változó:

- részleges eltérés a funkció;

- részleges eltérés a funkció;

- teljes eltérés funkciót.

Legyen egy függvény két változó definiált hallgatólagosan. . Ha vannak folyamatos származékok, és az implicit függvény részleges származékok által meghatározott képletek:

Érintő sík felületén egy ponton (érintési pont) egy síkban, amely az összes az ív érintője átszívott a pont a felületen.

Normál a felszínre a ponton az úgynevezett merőleges vonal a érintő sík azon a ponton, és átmegy az érintési pont.

Ha a felület nem adunk meg explicit, akkor az egyenlet a érintő sík ponton van a forma:

és a rendes egyenletet:

Ha a felület hallgatólagosan, az egyenlet a érintősík a lényeg a következő formában:

és a rendes egyenletet:

Szélsőértékében feladatokat a két változó.

Egy pont az úgynevezett minimum pont a funkciót, ahol ha egy bizonyos pont szomszédságában az összes egyenlőtlenség.

Egy pont az úgynevezett maximális pont a funkciót, ahol, ha egy bizonyos pont szomszédságában az összes egyenlőtlenség.

minimális és maximális pontot nevezzük pontok extrém funkciókat.

Ennek szükséges feltétele extrémuma. Ha differenciálható függvény egy szélsőséges azon a ponton, hogy a parciális deriváltak és ezen a ponton nullával egyenlő:

A pontok, ahol a parciális származékok a funkció és nulla, az úgynevezett stacionárius.

Kritikus pont az a pont, ahol a parciális deriváltak és nulla vagy legalább egy közülük nem létezik.

Elégséges feltétele szélsőérték. Let - kritikus pont. Jelöljük az értékeket a második származékok, és. majd

1) ha a - pont szélsőérték a függvény, és - a maximális pont és - legalább ponton;

2) Ha, akkor nincs szélsőérték;

3) Ha, akkor további vizsgálat szükséges.

Alapvető módszerek integrációját.

I. Közvetlen integráció az, hogy ez az integrál, hogy egy vagy több táblázatos integrálok segítségével tulajdonságait a határozatlan integrál, és különböző képletek (beleértve a trigonometrikus) és azonos algebrai átalakításokat integrandust.

II. A módszer társítása jele eltérés találni, vagy hozzon létre egy funkciót integrál, hogy minden az integrandus rögzítjük egy dedikált funkció:

III. változó helyettesítő módszer a következő egyenlet szerint:

IV. Hagyja, hogy a funkciók és folyamatos együtt származékai, akkor megvan a képlet integrálás:

Integrálás formula alkalmazható bármely folytonos függvények, de lehetővé teszi, hogy hatékonyan számítani a határozatlan integrál csak különleges műveleti osztályok:

1. Ha az integrál a következő formában:

, ahol - polinom foka

majd ahogy kell venni, és hogy a többi tényező az integrandus, azaz

2. Ha az integrál a következő formában:

, ahol - polinom foka

akkor, és minden mást, ami

3. Ha az integrál a formában: vagy a képlet a integrálás, ebben az esetben kétszer alkalmaztuk, akkor a kezdeti szerves expresszálódik algebrailag. Ez a ciklikus integráció.

V. integrációja racionális frakciók.

A kifejezés a forma, és ahol - két fokkal és polinom, illetve (és - természetes számok) egy racionális frakciót. Ebben az esetben, ha a frakció az úgynevezett helyes. Ellenkező esetben, ha - a frakció az úgynevezett nem megfelelő.

Egyszerűen jobb racionális frakciói:

1) - az elemi drobyuIvida;

3) - az elemi drobIIIvida (- nincs valós gyöke, azaz);

4) - az elemi drobIVvida (- nincs valós gyöke;).

Minden megfelelő frakció képviseletében összegeként véges számú részleges frakciók. Ebben az esetben, ha a nevező tényezőként:

ahol - a természetes számokat, majd

Vezetési integráció racionális frakciói:

Ha nem megfelelő frakció, szükséges bemutatni, hogy egy többtagú összeg és a megfelelő frakció;

Táguló nevezője racionális szám helyesen faktoring és képviseli azt összegeként a legegyszerűbb racionális frakciók;

Integrálja polinom, és a kapott összeg részleges frakciók.

VI. Integrálása irracionális funkciókat.

1. számítása integrálok a következő formában:

ahol - egy racionális függvény - egész - állandó valós szám.

Ez az integrál kiszámítása helyettesítve

2. számítása integrálok a következő formában:

ahol - a természetes számok.

Az integrál kiszámítása helyettesítve

ahol - a közös nevező a frakciók. A szerves könnyebb lesz, ha - a legkisebb közös nevező e frakciók.

VII. Az integráció egyes kifejezések, amelyek a trigonometrikus függvények.

1. Ha a integrandust felírható a termék a még hatáskörét szinusz és koszinusz, és a legalább egy indikátor negatív, az átalakítás után nyerhető alatt a beépített függvény vagy eltartott, majd integrálni, tekintettel arra, hogy

Ez a helyettesítés használjuk, ha az integrandus racionális függvénye, ugyanakkor

Ha az integrandus előjelet csak akkor változik, hogy, azaz =, akkor alkalmazza a cserét. Ebben az esetben,

Ha az integrandus előjelet csak akkor változik, hogy, azaz =, akkor alkalmazza a cserét. Ebben az esetben,

5.Vychislenie integrálok

Néhány speciális esetekben:

a) Legyen a szinusz és koszinusz ugyanezen érvek, ebben az esetben, és - nem negatív egész számok, és legalább egyikük páratlan.

Ha - egy páratlan szám, akkor az integrál kényelmesen kiszámítani szubsztitúcióval. Úgy használja fel az átalakulás az integrandus.

Ha - egy páratlan szám, akkor az integrál lehet kiszámítani szubsztitúciós. Ugyanakkor.

b) Ha a - még a nem-negatív szám, akkor a számítás az integrál kényelmes, hogy átalakítsa a integrandust képlet segítségével „csökkentés mértéke”, és a szinusz a kettős szög:

6.Vychislenie integrálok termékek trigonometrikus függvények:

Kiszámításakor a integrálját ez a forma kényelmesebb cserélni a terméket funkciókat az összeget, a következő egyenlettel:

7.Universalnaya trigonometriai helyettesítés:

Ezzel a helyettesítés megkapjuk

Intervallumon folytonos függvény definiálva. A hossza tetszőleges pont van osztva részleges szegmensek, ..., és - a legnagyobb a Ezen szegmensek hossza: ahol. Point - tetszőleges pontot a szegmensben. Aztán, ha a kumulált van egy határ, és nem függ a módszer partíció szegmens vagy kiválasztásával pont (), ez a korlát az úgynevezett határozott integrál függvény az intervallum:

Az alapvető tulajdonságait a határozott integrál:

Számítási módszerek határozott integrál.