Hogyan lehet megtalálni a gömb sugarának

gömbsugárral (jelöli, R vagy R) - egy szegmens, amely összeköti a közepén a labdát bármely pontján a felületén. Mivel abban az esetben, egy kör, a gömb sugarának fontos mennyiséget, amely szükséges megtalálni a labdát körtérfogat felülete és / vagy térfogat. De a labdát, és a sugár megtalálható a jelen értéke a körtérfogat és a többi értéket. A következő képlet, amely helyettesítheti ezeket az értékeket.

lépések szerkesztése

1. módszer 3:
Képletek kiszámításához a sugár szerkesztése

Számítsuk ki a sugara az átmérő. A sugara egyenlő átmérő fele, azonban, használja a képlet R = D / 2. Ez ugyanaz a képlet kiszámításához felhasznált a kör sugara és az átmérő. [1]

• Például, adott egy labdát átmérője 16 cm sugarú gömb :. R = 16/2 = 8 cm, ha az átmérő 42 cm, a sugár 21 cm (42/2 = 21) ..

Számítsuk ki a sugara a kerületén. Felhasználási képlet: R = C / 2π. Mivel a kerületi hossza C = πD = 2πr, felosztják a képlet a kerületi hosszúságú a vételi 2π, és a képlet megtalálásához a sugár. [2]

• Például, adott egy tálba egy kerülete 20 cm sugarú gömb :. R = 20 / 2π = 3183 cm.
• Ugyanez a képlet használható a sugarának kiszámítására és a kerülete a kör.

Számítsuk ki a sugara a gömb térfogata. Felhasználási képlet: R = ((V / π) (3/4)) 1/3. [3] A kötet a labda képlet szerint kiszámított V = (4/3) πr 3. izolátum r egyik oldalán az egyenlet, akkor kap a képlet ((V / π) (3/4)) = Z 3, azaz térfogatának kiszámításához sugarú gömb osztva π, az eredmény szorozva 3/4, és az eredmény hatványát 1/3 (vagy kocka gyökér kivonatot). [4]

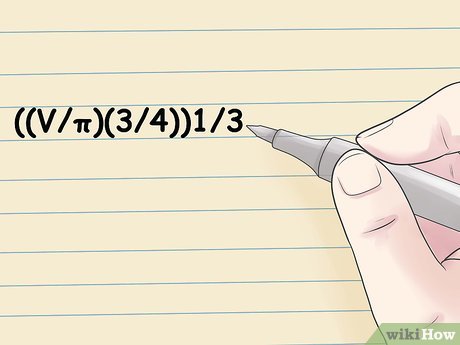
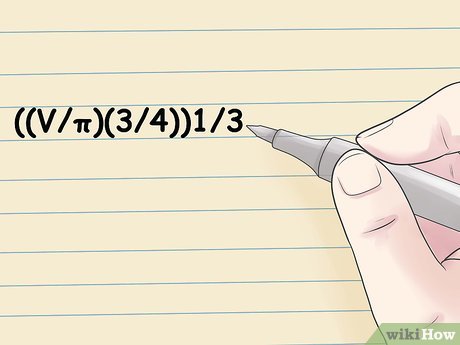
• Például, adott egy tálba egy térfogata 100 cm 3. Az a gömb sugarának a következőképpen számítjuk ki:
  • ((V / π) (3/4)) 1/3 = r
  • ((100 / π) (3/4)) 1/3 = r
  • ((31,83) (3/4)) 1/3 = r
  • (23,87) 1/3 = r
  • 2,88 cm = r

Számítsuk ki a sugara felület. Felhasználási képlet: R = √ (A / (4 π)). A felület egy gömb képlettel számítjuk ki: A = 4πr 2. izolátum r egyik oldalán az egyenlet, kapsz képletű √ (A / (4π)) = r, azaz, hogy kiszámítja a sugár, hogy a négyzetgyöke a felület osztva 4π . Ahelyett, hogy eltávolítja a gyökér, az expresszió (A / (4π)) lehet emelni, hogy a hálózati 1/2. [5]

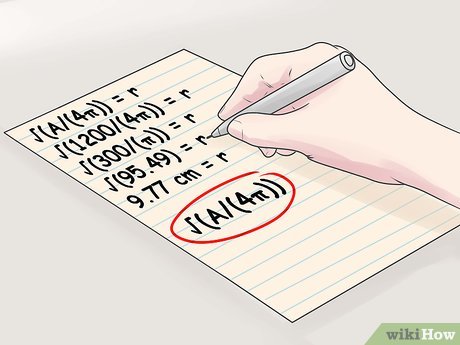
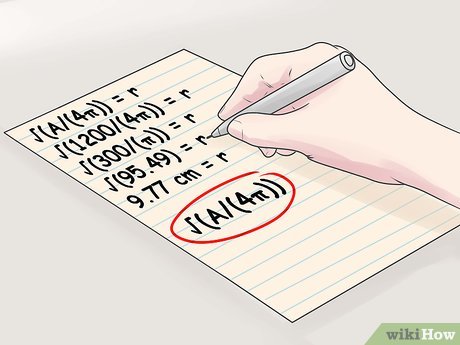
• Például, adott egy tál felszíni területű 1200 cm 3. A gömb sugarának a következőképpen számítjuk ki:
  • √ (A / (4π)) = r
  • √ (1200 / (4π)) = r
  • √ (300 / (π)) = r
  • √ (95,49) = r
  • 9,77 cm = r

2. módszer 3:
Meghatározása alapmennyiségekre szerkesztése

Megjegyzés alapmennyiségekre, amelyek relevánsak a számítás sugara a labdát. sugara a labda - egy szegmens, amely összeköti a közepén a labdát bármely pontján a felületén. A sugara a labda alapján kell kiszámítani az értékeket a körtérfogat felszíni területet vagy térfogatot.

• Az átmérő (D) - egy szegmens, amely összeköti a két pont a gömb felülete és közepén halad át (azaz, ez a legnagyobb távolság közötti szemközti elhelyezkedő pontok az a gömb felszínén). Az átmérő kétszerese a sugár.
• A kerülete (C) ábra egy hossza egy nagy kör, vagyis a kör, amely képezi a vágási sík közepén keresztül a labda.
• A térfogat (V) - az értéke háromdimenziós térben elfoglalt el. [6]
• A felület területe (A) - a értéke kétdimenziós (planáris) által meghatározott tér a labdát felületi.
• Pi (π) - egy állandó, amely az arány a kerülete és átmérőjének. Első tíz számjegye ennek konstans 3,141592653, de gyakran a pi szám felfelé kell kerekíteni 3,14.

A következő adatok értékeit a mennyiségek, hogy megtalálják a sugara. A sugár alapján lehet kiszámítani, hogy az értékek a körtérfogat felszíni terület és térfogat. Sőt, ezek az értékek találhatók egy adott érték a sugár. Kiszámításához sugár, csupán átalakítani formulákat találni ezeket az értékeket. Az alábbiakban a képlet (amelyben van egy sugár) kiszámítására körtérfogat felszíni terület és térfogat.

• D = 2r. Akárcsak a kör átmérője a labdát kétszer sugara.
• C = πD = 2πr. Mivel abban az esetben, egy kör, a kerülete hossza a labda egyenlő a termék a π a labda átmérője. Mivel az átmérője kétszerese a sugara a labda kerülete egyenlő kétszerese a termék a π a gömb sugarának.
• V = (4/3) πr 3. A kötet a labda egyenlő a termék a π és 4/3 sugarának harmadik hatványával. [7]
• A = 4πr 2. Az felülete a labda egyenlő négyszer a termék a π sugarának négyzetével. Mivel a terület a kör πr 2. A labda felülete négyszerese a terület egy kör képező részén áthaladó sík közepén a labdát.

Kapcsolódó cikkek

• Nadya Mikhalkov talált terhelő bizonyítékokat az okostelefon férje

• Hogyan lehet megtalálni a csekk száma

• Hogyan talál hivatását, megtudja az igazságot! (Com)