Hogyan építsünk egy háromtagú négyzeten - hogyan rakja az összeg a téren - Matematika

Megoldásában a számtani és algebrai problémák néha szükség van, hogy építsenek egy töredéke a téren. A legegyszerűbb módja ennek, ha egy tizedes törtet - csak egy hétköznapi számológépet. Azonban, ha a frakció rendes vagy vegyes, egyes nehézségek merülhetnek fel az építkezés során ilyen számokat a téren.

• számológép, számítógép, Excel alkalmazás.

Ahhoz, hogy épít egy tizedes törtet a téren. Vegyünk egy tudományos számológép, írja emelt kvadratdrob, és nyomja meg az építőiparban a második fokozatot. Ez a gomb a legtöbb számológép kijelölt „h²”. A szabványos Windows számológép funkció négyszögesítése úgy néz ki, mint a «x ^ 2" . Például, a tér a tizedes egyenlő 3,14: 3,14² = 9,8596.

Tér a tizedes egy normál (könyvelés) számológép, szorozza meg ezt a számot is. By the way, egyes modellekben a számológépek lehetőséget adott számos emelt négyzet hiányában is egy dedikált gomb. Ezért előre olvasási utasítást adott számológép. Néha példák „ravasz” hatványozó látható a hátlapot vagy a számológép mezőbe. Például számos számológépek az építőiparban a tér, csak nyomja meg az „x” gombot, és a „=”.

A négyszögesítése közös frakciót (amely a számláló és a nevező), emelkedett, hogy egyenként négyzetes számláló és a nevező az a frakció. Ez azt jelenti, használja a következő szabály: (c / o) ² = ch² / ZZ ahol h - a számlálóban, s - drobi.Primer nevező: (3/4) ² = 3² / 4² = 9/16.

Ha épített belső kvadratdrob - vegyes (áll egy egész részét, és a közös frakció), az előre hozza, hogy a rendes elme. Azaz, az alábbi képletet alkalmazza: (n c / o) ² = ((n * h + H) / h) ² = (s + n * h) ² / ZZ ahol n - az egész része a kevert drobi.Primer: (3 2/5) ² = ((5 * 3 + 2) / 5) ² = (3 * 5 + 2) ² / 5² = 17² / 5² = 289/25 = 11 14/25.

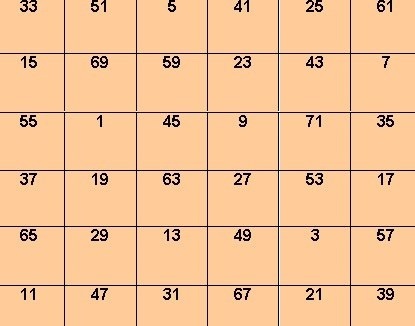
Matematikai feladványok néha elviszik, hogy szeretnék megtanulni, hogyan kell létrehozni őket, nem csak megoldani. Talán a legérdekesebb a kezdők, hogy egy mágikus négyzet, amely egy oldalú négyzet méretei nxn amelyen fel van tüntetve a természetes számok 1-től n2 úgy, hogy a számok összege vízszintes vonalak, függőleges és átlós négyzet azonos, és egyenlő egy számot.

Mielőtt a téren, megértjük, hogy másodrendű mágikus négyzetek nem történik meg. Harmadrendű bűvös négyzet van valójában csak egy, a másik az ebből származó kapunk forgatással vagy tükrözi a fő szimmetria tengelye a téren. Minél több rend, annál van egy lehetséges mágikus négyzetek rend.

Ismerje meg az alapokat az építés. Szabályai építése különböző mágikus négyzetek három csoportba oszthatjuk rendje szerint a tér, vagyis ez lehet furcsa, kétszeresével egyenlő, vagy négyszer a páratlan szám. Általános eljárás az építőiparban minden négyzet jelenleg nem létezik, bár igen különböző rendszereket.

Használjon egy számítógépes program. Töltse le a kívánt alkalmazást, és a kívánt értéket a tér (2-3), a program generálja a kívánt digitális pályára.

Készítsd el a saját tér. Vegye ki a mátrix n x n. belül, amelyek az építőiparban a lépcsős rombusz. Ebben töltse ki az összes négyzetet a bal fel minden átló sorozatából páratlan számok.

Határozzuk meg az értéke a központi cella A. a sarkoknál a bűvös négyzet az ilyen pozíció: jobb felső cella - O-1, bal alsó - D + 1, jobbra alul - O-N, és a bal felső - O + n. Üres cellák a szögek a háromszögek töltse segítségével meglehetősen egyszerű szabály: a sorok balról jobbra, hogy növelje az n + 1, és a bárokban az irányba felülről lefelé, hogy növelje a száma az n-1.

Fedezze fel az összes négyzetet a sorrendben egyenlő n csak akkor lehetséges, ha n \ le 4, annyira érdekes külön eljárások építésére mágikus négyzetek n> 4 A legegyszerűbb módja annak, hogy kiszámítja a design a tér páratlan rendű. Kihasználni a speciális formula, ahol szeretné, hogy csak tegye meg a szükséges adatokat, hogy a kívánt eredményt.

Például, egy állandó tér, beépített program keretében rizzsel. 1 képlettel számítottuk ki:

S = 6A1 + 105b,
ahol a1 - az első tagja a progresszió,
b - a különbség progresszió.