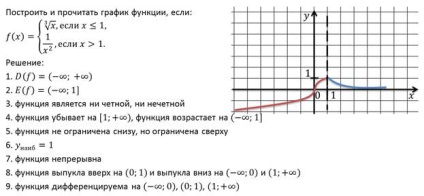
gyökér funkció
A gyökér n-fokú nemnegatív szám negatív szám, ha emeljük az n-menetek száma, amelyek mértékét a.
A gyökér a páratlan n-fokú negatív számok az úgynevezett negatív szám, ha emeljük az n-menetek száma, amelyek mértékét a.
Ahol n - indikátora a gyökér, és egy - egy radicand.
Így minden gyökér-kivonat (a második és több) lehet bármilyen nem-negatív számok, és egy negatív számot kivonjuk gyökér csak páratlan fokú.
A [0; + ∞) lehet szállítani, minden számot x szerinti Singular gyökere fokú N-x bármelyik értéke n.
Ez azt jelenti, hogy a forgatáson [0; + ∞) beszélhetünk a gyökér funkció:
Most határozza meg a tulajdonságait ezt a funkciót, és szerkesszük a grafikonon.
Az alapvető tulajdonságait funkciók:
A [0; + ∞) - a domain.
Mivel a nem-negatív szám a gyökere n-fokú, nem-negatív szám, akkor a [0; + ∞) a domain függvény értékei.
Mivel a szimmetrikus halmaz nem a domain a funkció, így a funkció nem páratlan és nem is.
A művelet kitermelése a gyökér adjuk inverz művelet emelése megfelelő mértékben.
Tehát azt lehet mondani, hogy:
Most megadhatók a gyökér funkciót.
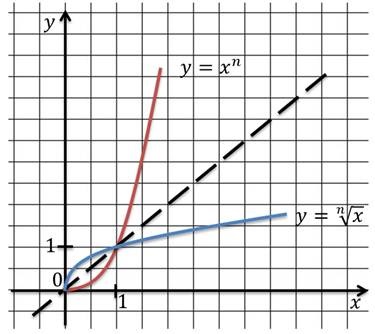
A grafikon, tudjuk írni a maradék tulajdonságait a funkciót.
A [0; + ∞) funkció növeli.
Top funkció nem korlátozott, de ez korlátozott alulról, például egy egyenes vonalat, amely = -0.5.
Az egész tartomány a függvény konvex, felfelé irányuló.
Mi jellemző a legalacsonyabb érték 0 lesz, és a legnagyobb érték van.
Ha az egyes pontok bizonyos intervallum függvény differenciálható, az azt jelenti, hogy egy adott időszakban folyamatos.
Bármely pontján a [0; + ∞) létezik, ez a származék, az egyetlen kivételt az a pont 0. Mivel bármely pontján a (0; + ∞) függvény egy származékát, azt jelenti, a (0; + ∞) függvény differenciálható.
Tekintsük néhány példa a grafikonok gyökér funkciót.
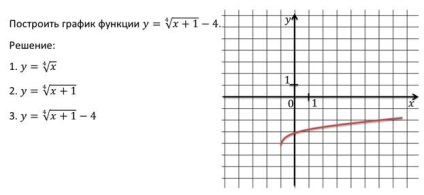
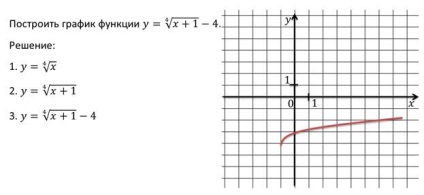
Ezek a példák érintik a funkciót, amelyben Y jelentése gyökere fokú N-X, csak a nem-negatív értékek az érvelés.
De ha n páratlan szám, akkor a negatív x is a kifejezés jelentését n-fokú gyökere x. Szóval, akkor lehet beszélni a funkciót:
Jegyezzük fel a tulajdonságait ezt a funkciót.
Span (- ∞; + ∞) az a tartomány a függvény.
Span (- ∞; + ∞) az értéktartomány.
A domain a funkció egy szimmetrikus sor, akkor ez a funkció lehet tanulmányozni paritás:
Látjuk tehát, hogy a funkció páratlan páratlan n.
Építünk a függvény grafikonját.
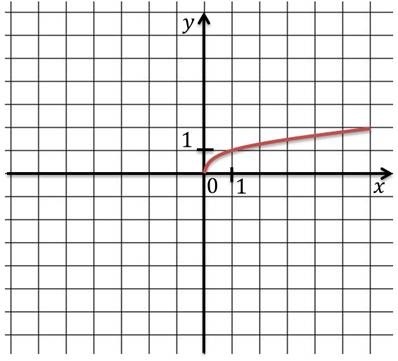
Ehhez hozzátesszük ág területén fiókteleppel, hogy szimmetrikus a származás, erre használjuk a tulajdonsága páratlan gyökér funkciót.
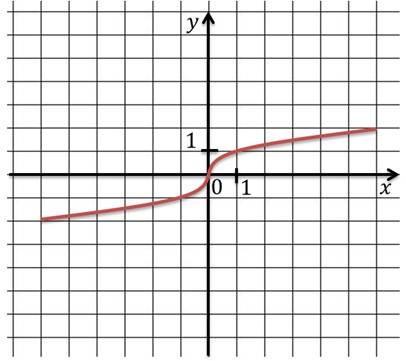
- A kapott grafikon segítségével könnyedén rögzíti a maradék tulajdonságait a funkciót.
- Az egész tartomány a függvény növekszik.
- Sem a felső, sem az alsó a funkció nincs korlátozva.
- Függvény nem rendelkezik a legmagasabb és a legalacsonyabb érték.
- Az egész tartomány a függvény folytonos.
- Az intervallum (- ∞; 0) konvex lefelé, és a (0; + ∞) konvex felfelé.
- Az egész tartomány a függvény differenciálható, kivéve a 0 pont.
Még néhány példa a grafikonok gyökér funkciót.