Gyakorlati alkalmazási № 3
Fogalmak: vektor a mágneses indukció, a mágneses erővonal, a szuperpozíció elve a mágneses mező, jobb kéz szabály, erő Amper, elektromos és mágneses komponense a Lorentz-féle erő, a mágneses momentuma a hurok egy aktuális, a jelenség a elektromágneses indukció, indukált elektromotoros erő, ami az indukciós áram, tipikusan Lenz, örvény elektromos mező.
tesztkérdések
1. Hogyan határozza meg az irányt, és nagysága a mágneses indukció a tér kísérleti módszerek?
2. Milyen egységekben mérik a mágneses indukció SI-rendszer?
3. Mi az amper?
4. Fogalmazza Amper törvénye.
5. Hogyan kell meghatározni a Amper ható erő áramvezető tetszőleges alakú?
6. Mi a Amper ható erő zárt körben, ahol az áram egy homogén mágneses mezőt?
7. Mi a mágneses momentuma az áramkör? Hogyan állapítható meg, annak irányát?
8. Hogyan kell meghatározni az időben Amper ható erő az áramkört az áram egyenletes mágneses mezőt?
9. Mi az elektromos és mágneses komponense a Lorentz-erő?
10. Mi az a jelenség, az elektromágneses indukció?
11. Fogalmazza meg a törvény az elektromágneses indukció.
12. Mi a szabály Lenz irányának meghatározásához az indukált áram?
13. Mi az örvényáramok?
14. Mi a működési elve a generátor és a transzformátor áram?
Példák problémák megoldása
Probléma 1. Két hosszú egyenes párhuzamos drótokból található a parttól r = 5 cm-re egymástól. Átfolyó áramok huzalok I1 = I2 = 10 A. megtalálni a mágneses indukció a pont, található a parttól r1 = 4 cm-re az első vezeték és r2 = 3 cm-re az utóbbi.
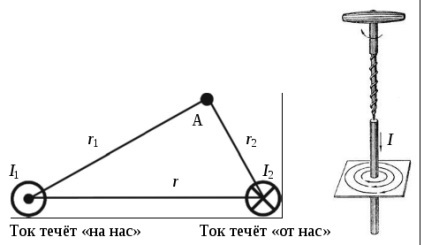
Hosszú, egyenes vezeték, amelyen keresztül áram folyik I. létrehoz egy mágneses mezőt maga körül a régióban R indukcióval:
ahol - mágneses állandó. Az irány a mágneses indukció vektor ebben az esetben meg lehet határozni a jobb kéz szabályt, hogy ha transzlációs mozgása hüvelykujj (jobbmenetes csavar) van irányítva, egy aktuális irányba, a forgó mozgást - abba az irányba, a mágneses erővonalak. mágneses indukció vektor tangenciálisan irányított mágneses erővonal.
Háromszög oldala 3, 4, 5 cm-es téglalap alakú, és így a bezárt szög a vektorok
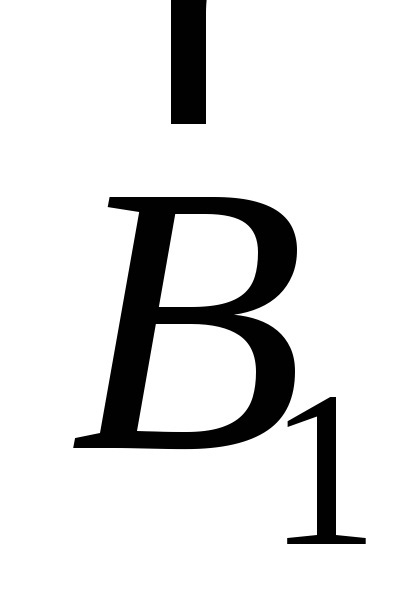
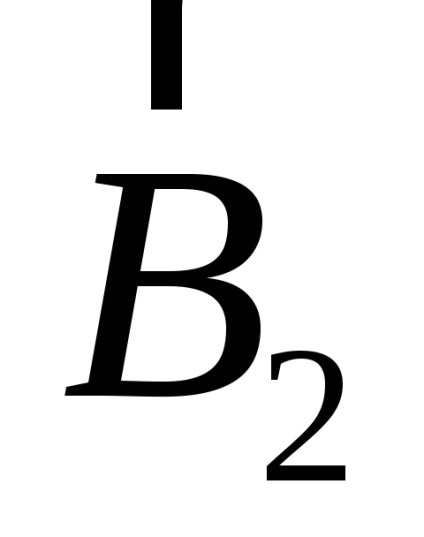
W
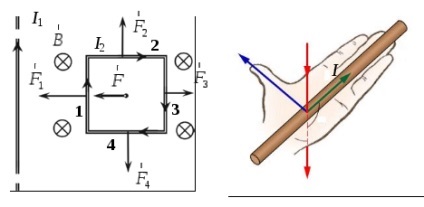
Határozat. Az I1 áram olyan mágneses mezőt, amely hat a keret a jelenlegi. Határozza meg az ökölszabály, hogy a mágneses indukció
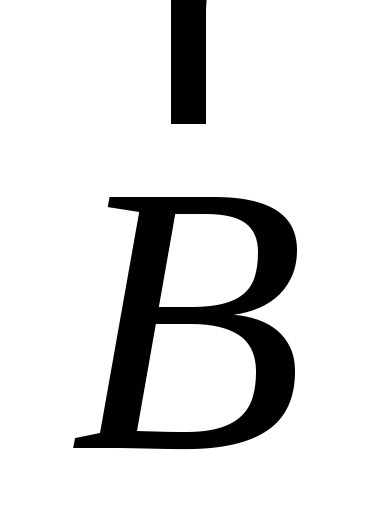
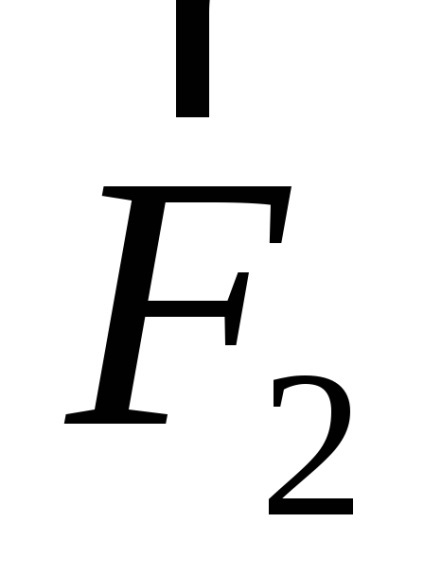
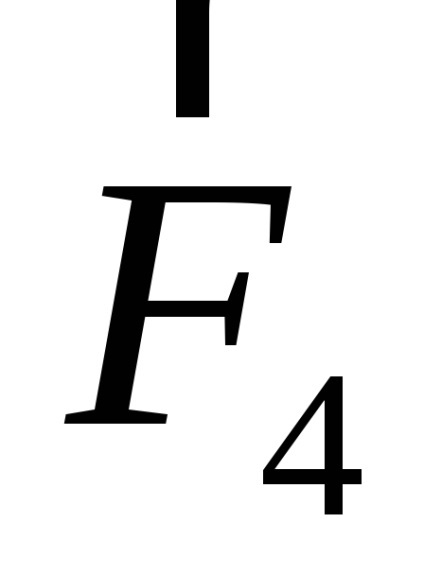
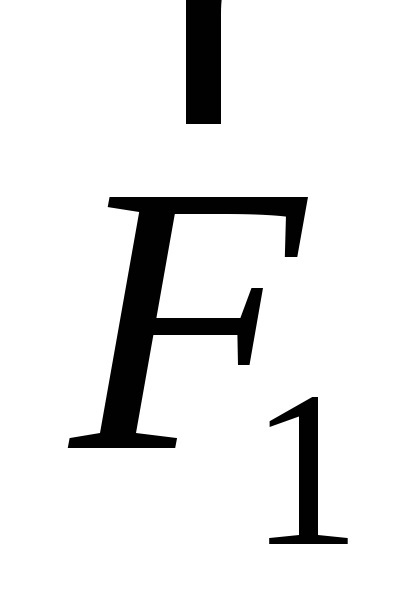
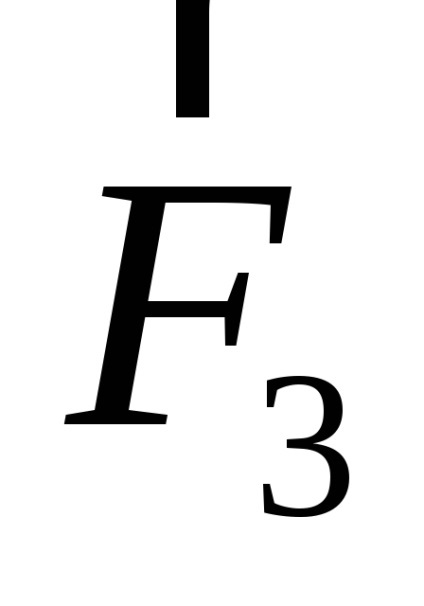
Ha egy egyenes huzal hordozó I áram van egy L hosszúságú és tárolni homogén mágneses mező B. irányul c indukciós szög az áram irányára, akkor úgy viselkedik, Amper erő egyenlő modulo:
Képlet alkalmazásával (2.1) és (2.2) a vezetékek 1 és 3, megkapjuk:
net erő
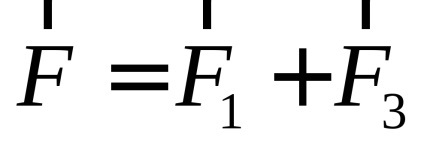
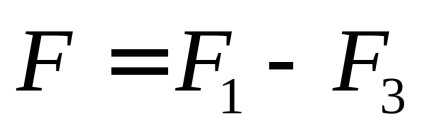
W
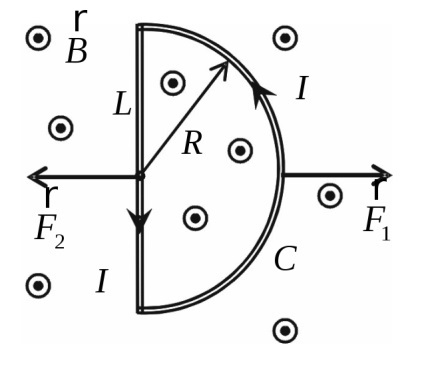
Határozat. Semiring C - egy nyitott áramkört, és az egyes áramköri elem egy aktuális
A kapott minden erő lehet meghatározni integráció:
Azonban, tekintettel arra, hogy a huzal egy homogén mágneses mezőt, ez az erő lehet meghatározni használata nélkül az elemek az integráció. Mi teljes félkört C egyenes vezető L. Ezután kapsz egy zárt kör, amelyen keresztül folyik áram I. Köztudott, hogy az Amper ható erő zárt körben, ahol az áram egy homogén mágneses mezőben nulla. ennélfogva
Alkalmazása Ampere törvénye, így lineáris vezető L.
W
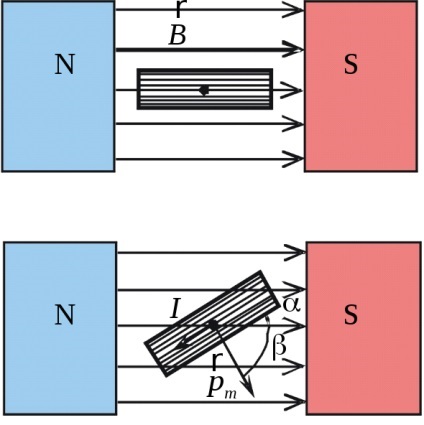
Határozat. Ha a jelenlegi keresztül a galvanométer nem szivárog, a keretre lesz orientált, amint az a fenti ábrán. Ha egy elektromos áram halad át a drót köré tekert galvanométert keret, van egy pillanat erő Amper MA. amely bekapcsolja a keret, ameddig egyensúlyban van a pillanat Mupr rugalmas erők. felmerülő izzószál egy olyan szöggel a , az alábbiak szerint. Nyomaték Amper formula határozza meg:
ahol pm = ISN - mágneses momentuma tartalmazó hurok N fordul, - közötti szög a mágneses pillanat és a kontúr a mező vektora a mágneses indukció, ahol az áramkör: = 90º - = 60 °. Abban a pillanatban, hogy a rugalmas erő arányos a szög a csavart fonal:
ahol C - állandó torziós szálat. Ha az egyensúly a keret a jelenlegi,
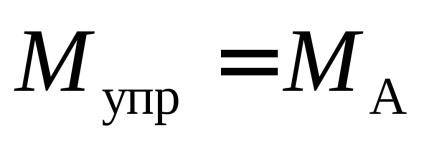
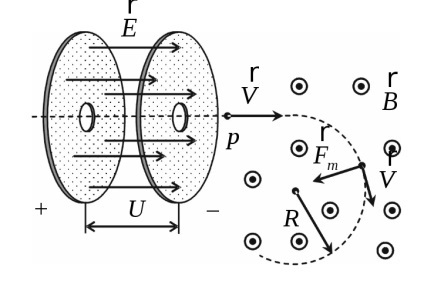
Határozat. Amikor a proton átmegy a gyorsuló potenciális különbség U. működteti a villamos eleme a Lorentz-erő (elektrosztatikus erő)
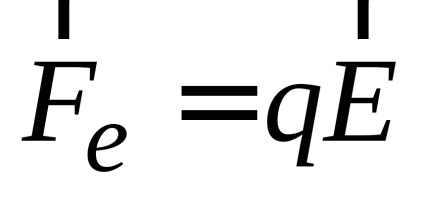
ahol m és e - a tömegét és töltését egy proton. Így:
Ezután a proton kap egy homogén mágneses mezőben, és elindul egy kört. A mágneses komponens a Lorentz-erő
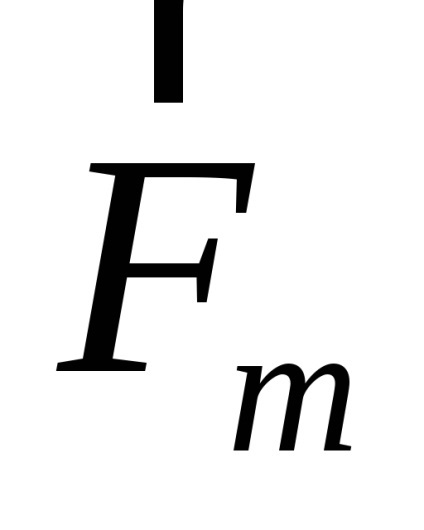
- közötti szög a részecskesebesség
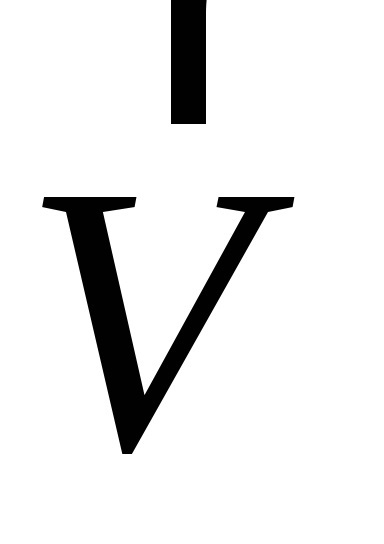
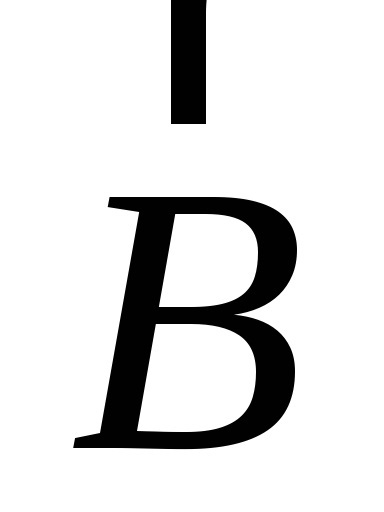
Miután konvertáló a kifejezéseket (5.4) kapjuk:
Feladat 6. repülőgép sebessége V = 950 km / h. Find a potenciális különbség , előforduló végei között a szárnyak a repülőgép, ha a függőleges komponense a földfelszíni mágneses indukció a mező B = 310 -5 Tesla és hatálya repülőgép szárnya L = 12,5 m.

Feladat 7. szál gyűrű sugara r = 10 cm az asztalra. Mi a Q töltésű cseppek a gyűrűn keresztül, ha a kanyarodás egyik oldalról a másikra? Az R ellenállás a gyűrű egyenlő 1 ohm. A függőleges összetevője az indukciós a föld mágneses mező 50 mT.
Határozat. Miután által határolt területen a huzal gyűrű, a mágneses fluxus halad 1 = B r 2. Ha a gyűrű elfordul a másik oldalon, a mágneses fluxus változások az ellenkező megjelölés: 2 = -1. Mivel a gyűrű el van forgatva, a mágneses fluxus áthatoló annak változását. Ez ahhoz vezet, hogy az indukciós EMF:
Következésképpen, a energizált indukciós áram gyűrű:
Használata (2.1) és (2.2), mi származik a differenciálegyenlet megoldása azt:
Válasz: Q = 3,14 SCLC.
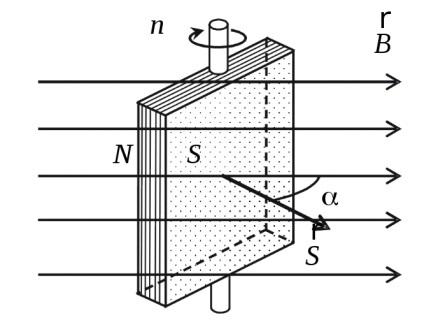
8. feladat a kereten területen S = 200 cm 2 köré tekercselt N = 100 huzalmenetre. Ez forgatja egyenletesen gyakorisága körülbelül n = 10 / képest egy tengely síkjában fekvő, a keret és a vonalakra merőleges irányban a mágneses mező (B = 0,2 T). Keresse meg a maximális indukált elektromotoros felmerülő vezetéket. Határozzuk meg a maximális indukált áram, ha az ellenállás huzal R = 5 ohm.
Határozat. A mágneses fluxus behatol a keret, amelyen fel van tekercselve egy vezetéket, az idő változik forgása következtében a keret:
Ezért a keret a EMF indukciós:
Ebből következik, hogy a maximális indukált elektromotoros erő felmerülő a keret egyenlő:
Ezután a legnagyobb indukciós áram: