Geometry feladat
Nagyon sok ilyen problémákat megoldani az építési további (Tuning-, ragaszkodik.). Meg kell, hogy egy másik ugyanolyan prizma, „fel”, hogy az eredeti. A felső pont a hozzáadott prizma jelöljük az azonos betűket indexe 2, azaz a A2, B2 és C2. Ez azonnal nyilvánvaló, hogy a kívánt sík (AKS) része AV2S a háromszög síkjában, és hogy a P pont a közepén A1B1.
Továbbá, a távolság BH legkönnyebb meghatározni térfogat AVSV2 piramis. Ha tekinteni, mint egy piramis alapsík az ABC háromszög, (BB2 magasság = 6), a hangerő
Másrészt, mivel az alapja a piramis lehet tekinteni sík AV2S háromszög, mivel VN - a magassága a piramis. Továbbra is számítani a háromszög területét AV2S. Ő egyenlő szárú. Fél AB2 és CB2 könnyen kiszámítható Püthagorasz és egyenlő √40. Magasság is Püthagorasz is √39. Tehát AV2S területe a háromszög (1/2) * 2 * √39 = √39. Ezután HV = 6√3 / √39) = 6 / √13 = 1,664100589
Felejtsd el egy pillanatra a prizmát. Két párhuzamos sík bázisok. Metszik a harmadik (APKC). Vonalak metszéspont a referencia sík párhuzamos egymással. AS || PK || A1C1, itt az oldalán a felső bázis és A1B1 S1V1 osztva egyenlő arányban, mint a másik, és a magassága a háromszög. Ezért a „P” van építve.
Ilyen problémák legkényelmesebben megoldani a stílus ábrázoló geometria. Ha a rajz történik a megfelelő perspektívát. Ebben az esetben, figyelembe véve a szegmens végén hangszóró, úgy, hogy megjelenítse a BNN1B1 az ábra síkjából teljes méretben. De ma mellőzését izometria.
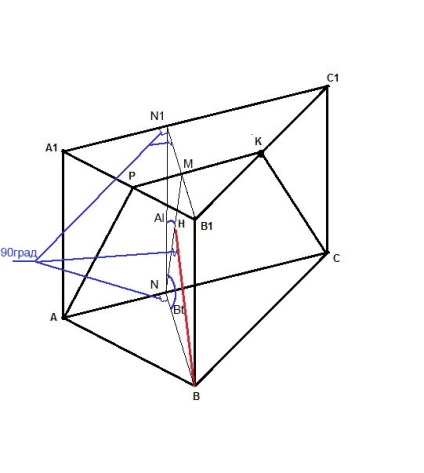
A legrövidebb távolság merőleges síkban enni, és ezért BH merőleges bármely egyenes síkjában fekvő, mint a NM.
Azt mondjuk, hogy a háromszög oldala „a”
A magasság „h”
prizma magassága a „G”
Ami jellemző, hogy a növekedés a G nem befolyásolja a számítás eredményét. És a jövőben BH arra törekszenek, hogy „h”.