feladatok 7
31. Az ábrán a grafikon y = f (x) és az érintő hozzá a ponton az abszcissza x0. Find az érték a származék az f (x) x0.
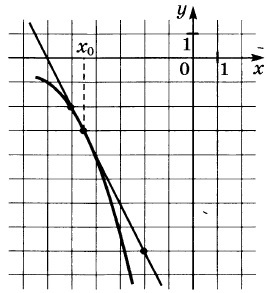
Megoldás: Az érték a származék az érintkezési pont megegyezik a lejtőn a tangens, amely viszont egyenlő a lejtőn a érintőleges az x-tengely. Construct egy derékszögű háromszög csúcsai pontokon A (-5; -2), B (-2; -8), C (-2; -2). A dőlésszög a érintőleges az x-tengely egyenlő a szög mellett a BAC szög.
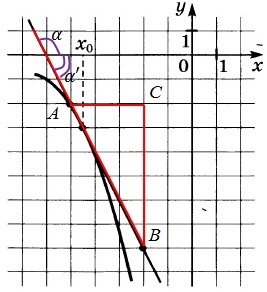
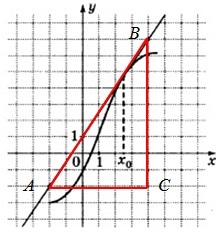
32. Az ábrán a grafikon y = f (x) és az érintő hozzá a ponton az abszcissza x0. Find az érték a származék az f (x) x0.
Megoldás: Az érték a származék az érintkezési pont megegyezik a lejtőn a tangens, amely viszont egyenlő a lejtőn a érintőleges az x-tengely. Construct egy derékszögű háromszög csúcsai pontokon A (-3; -3), B (5; -5), C (5; 3). A dőlésszög a érintőleges az x-tengely egyenlő a szög mellett a BAC szög.
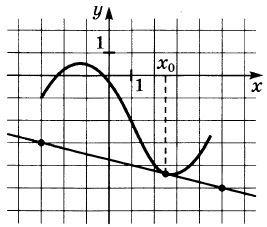
33. Az ábrán a grafikon y = f (x) és az érintő hozzá a ponton az abszcissza x0. Find az érték a származék az f (x) x0.
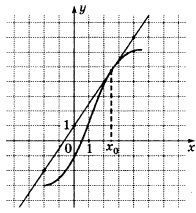
Megoldás: Az érték a származék az érintkezési pont megegyezik a lejtőn a tangens, amely viszont egyenlő a lejtőn a érintőleges az x-tengely. Construct egy derékszögű háromszög csúcsai pontokon A (-2; -2), B (4, 7), C (4, -2). A dőlésszög a érintője az X tengely egyenlő a BAC szög.
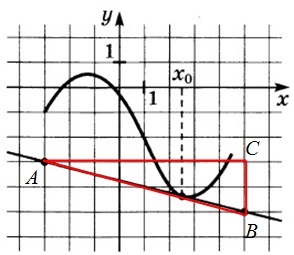
34. Az ábrán egy grafikon y = f (x) és a pontot jelöli -5, -3, 3, 7. néhány ilyen pontok legnagyobb értéke a származékos? Erre válaszul adja meg ezt a pontot.
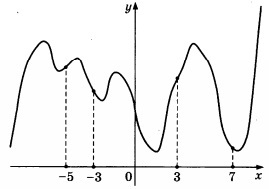
Megoldás: -3 pont és 7 működése csökken, majd ezt a származékot közülük negatív.
A 3. és -5 funkció növekszik, akkor a derivált pozitív bennük.
Aztán, úgy döntünk, a legnagyobb érték a származék pont 3 és -5.
Szerint a geometriai jelentése a származék: a származékot az érintkezési pont megegyezik a lejtőn a tangens, amely viszont egyenlő a lejtőn a érintőleges az x-tengely.
A dőlésszög (és annak tangens) egyértelműen nagyobb a 3. pontban, ezért, a származék ott a legnagyobb értéket.