Fejlesztése a folyamatábra a probléma megoldásának - a gyakorlati munka
választ teszt kérdéseire;
következtetések gyakorlati munka.
1.2. áttekintés
Az egyik leginkább munkaigényes szakaszában a probléma megoldásának a számítógép ki kell alakítani egy algoritmust.
Algoritmus által értjük a pontos recept, meghatározó számítási folyamat, ami változtatásával a kezdeti adatok a kívánt eredményt.
A fő jellemzője az algoritmus:
determinizmus (bizonyosság) - a megadott kezdeti által szolgáltatott adatok az egyediségét a kívánt eredményt;
tömeg - alkalmasság az ilyen típusú feladatot, ha a kezdeti adatok tartozó egy adott részhalmazát;
hatékonyságát - által végrehajtott egy számítási folyamatot hajtunk végre egy véges számú lépésben a kibocsátása értelmes eredményt;
diszkrét - a lehetővé tételét algoritmus külön szakaszban, amelynek végrehajtása nem kétséges.
A következő típusú számítási folyamatok:
Lineáris számítási folyamatot.
Az eredmény akkor kell végezni néhány műveletet egymás után.
Elágazó számítási folyamatot.
Az adott szekvenciát a műveletek függ értéket, egy vagy több paraméter. Például, ha a diszkrimináns a másodfokú egyenlet nem negatív, akkor az egyenletnek két gyöke, és ha negatív, akkor nincs igazi gyökereit.
A ciklikus számítási eljárás
Az eredmény egy lépéssorozatot kell végezni többször. Például ahhoz, hogy egy táblázatot az értékek egy előre meghatározott tartományban a vitát egy előre meghatározott pályán, hányszor kell határozni a következő érték az az érv, és kiszámítja az értékét funkciót.
Másfelől, ott is többféle számítástechnikai ciklikus folyamat. nevezetesen:
Számlálás ciklus (ciklusok az előre meghatározott számú ismétlések) - - egy ciklikus folyamatok esetén, ahol az ismétlések száma ismert.
Ciklusokat - egy ciklikus folyamat, hogy véget ér elérve vagy megsértése bizonyos feltételek mellett.
Keresés ciklus - egy ciklikus folyamat, amelynek van két kimeneti lehetőségek:
- hozam folyamat befejezése;
- korai nyugdíjazás minden további feltétel.
Típusa szerint számítási eljárás megvalósított algoritmus különböztethető meg:
- algoritmusok lineáris szerkezetű;
- elágazó struktúrák algoritmusok;
- gyűrűs szerkezetet algoritmusok.
Algoritmusok gyakorlati problémák megoldására általában kombinált szerkezet, azaz tartalmazzák mind a három típusú számítási folyamatok.
Révén vizuális leírása algoritmus a következő fő módszerek bemutatása:
- verbális (természetes nyelven bejegyzés);
- strukturális és stilizált (a felvételt a algoritmikus nyelv és pszeudo-kód);
- grafikai (image minták és grafikus szimbólumok);
- szoftverek (szövegek programozási nyelven).
A verbális módszer leírását az algoritmus leírása, egymást követő számozott adatok és adott tetszőleges bemutató természetes nyelv.
Az algoritmus hozzáadásának két szám (a és b).
Ask, mi az a szám a.
Ask, mi az a szám, b.
Fold a és b, az eredménnyel hozzárendelése.
Az eredményt.
A módszer előnye az egyszerűség leírás és a hátránya, hogy ez a megközelítés a bőbeszédű és nem szigorúan formalizált így lehetővé teszi egyértelmű értelmezése bizonyos követelményeknek, ahol egy verbális reprezentáció algoritmus módszer nem terjedt el.
Szigorú környezetben lévő adatfeldolgozó algoritmusok és azok szerkezetét szükséges, hogy legyen egy formális rendszer a jelképek és alkalmazott szabályokat érzékel semmilyen értelmezett rendelkezések pontosan és egyértelműen. Vonatkozó szabályait a rendszer nyelvi leírások. Ezek közé tartozik az algoritmikus nyelvek (pszeudo-kód), folyamatábrák és programozási nyelvek.
Szerkezetileg stilizált módon leírja egy algoritmus alapján a felvétel algoritmusok formalizált ábrázolása rendeletek által meghatározott használata korlátozott számú szabvány szintaktikai szerkezetek, gyakran nevezik pszeudo-kódot.
Az előny a közelség a pszeudo-kód programozási nyelvek és hátrányai, viszont a komplexitás a fejlődés és a lehetetlen közvetlen algoritmus bemenete megoldani egy számítógép, azaz lefordításának szükségessége egy programozási nyelv.
A grafikus módszer leírására algoritmus feltételezi, hogy a struktúráját leíró használt algoritmus beállítása a grafikus képek (blokkok) csatlakoztatható távvezeték ellenőrzés. Egy ilyen kép nevezik Blokkdiagramok.
Folyamatábra - grafikus ábrázolása a haladás a probléma megoldásának. A blokkvázlata áll blokkok vonalak kötik össze, és a blokkok jelennek formájában geometriai formák, az úgynevezett szimbólumokat. Belül egy karaktert írásos utasításokat a funkciókat, amelyeket a blokk - a képlet, szöveg, logikai kifejezések. A típus a karakter és a futás folyamatábrák szabványosított szabályok - GOST 19,701-90 tartalmazza a szimbólumok listáját, nevük megjelenített funkciók, formájú és méretű, valamint a végrehajtását a rendszer szabályai szerint. Amikor a fejlődő az algoritmus minden cselekvés jelölésére megfelelő blokkban mutatja azok szekvenciáját vonalak nyilak az egyik végén. A nevek, azonosítás és kijelölés elemek folyamatábrák ábrán látható. 1.1.
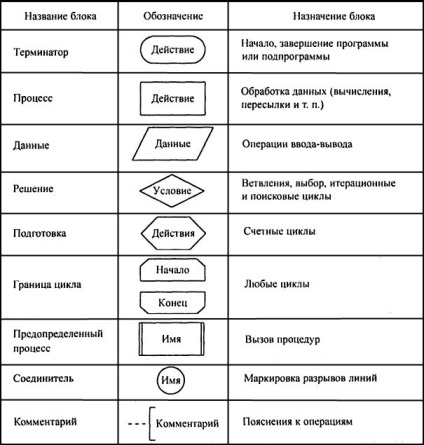
1.1 ábra - Basic Blocks
Érdemes megemlíteni néhány alapvető szabályait végrehajtó folyamatábrák kell követni a grafikus leírása algoritmusok. Kezdés algoritmusok jelölt „Terminator”, amelyből az egy sorban. Meg van írva a „Start” gombot ( „Home”). Vége algoritmus jelölt azonos szimbólumot, ahol az írott szó „Stop” ( „End”). Ebben az esetben, a karakter nem egy vonal kimenet, és lezárhatja egy vagy több vonal. A „folyamat” egy vagy több bemeneti vonal és csak egy kimenet. Bent a szimbólum több előírásokat lehet rögzíteni - ebben az esetben végrehajtásuk sorrendjét felvételt. Presentation egyes műveletek inkább szabadon. Utalni számítástechnika, akkor a matematikai kifejezések adatátvitelre - nyilak, egyéb intézkedések - magyarázza a természetes nyelvben, például az A = X + 4; i: = i + 1, -> B.
Írni az algoritmus a komplexitás csak három alapvető struktúrákat.
kövesse - képviseli a következetes végrehajtását az akcióban (lásd 1.2 ábra a.);
elágazási - megfelel a választott egy vagy két irányú (a 1.2 ábra B).
ciklus-ig - meghatározza az ismétlése akciók, amíg a feltétel megsértése, amelyek teljesítése ellenőrizzük elején a ciklus (1.2 ábra a.).
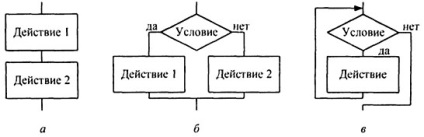
1.2 ábra - Basic algoritmikus struktúrák
Ezenkívül további algoritmikus szerkezeteket használnak a leírást az algoritmusok. a származékok a bázist, amelyek mindegyike lehet megvalósítani alapvető szerkezete:
kiválasztása - kiválasztja az egyik több lehetőség, attól függően, hogy a mennyiség értéke (ábra 1.3, és a b.);
ciklus-a - ismétlése egyes intézkedések teljesítette az előre meghatározott feltételt ellenőrzést, amely után végezzük a lépéseket a ciklus (1.3 ábra, d.);
egy gyűrű, amely egy adott számú iteráció (ciklusszámláló) - ismétlése egyes intézkedések meghatározott számú alkalommal (lásd az 1.3 ábrát, d, e.).
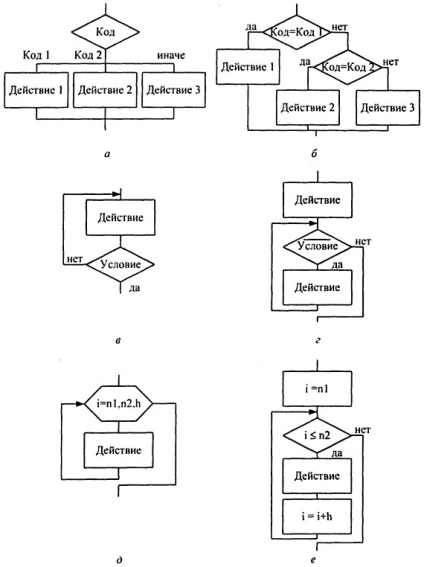
1.3 ábra - végrehajtása további algoritmikus struktúrák
szerte az alapstruktúra
Tekintsük a példák a grafikus leírások a különböző típusú algoritmusok: lineáris, elágazó, gyűrűs és kombinált (ábra 1,4-1,7.).
1.2 példa. Lineáris algoritmus.
Egy algoritmust kiszámítására expressziós értéke K = 3b + 6a (ábra. 1.4).
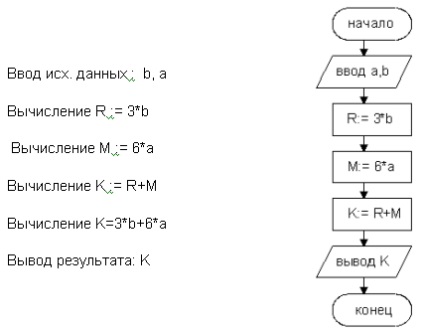
1.4 ábra - Példa folyamatábra lineáris algoritmussal
1.3 példa. Elágazás algoritmus.
Az algoritmus határozza meg, hogy a pass ütemezés funkció y = 3x + 4 ponton keresztül a koordinátákat x1, y1 (ábra. 1.5).
1.5 ábra - Példa flowchart elágazás algoritmus
1.4 példa. Körmérkőzéses.
Az algoritmus meghatározza a faktoriálisát természetes szám n (1.6 ábra.):
1.6 ábra - Példa folyamatábrák round robin
1.5 példa. Kombinált algoritmus.
Meg kell határozni a legnagyobb közös osztó két egész szám, A és B
A probléma megoldására az euklideszi algoritmus, amely jobban megfelel csere a számok a különbség a nagyobb és kisebb, míg a számok egyenlővé válik. Nézzük az algoritmus a két példát.
Példa (a): A = 225, B = 125. Alkalmazása az euklideszi algoritmus, megkapjuk az A és B, a legnagyobb közös osztó 25.
Példa (b): A = 13, B = 4. Ebben az esetben, a legnagyobb közös osztója a A és B jelentése megegyezik a 1.
Folyamatábra euklideszi algoritmus megtalálása a legnagyobb közös osztó két egész szám ábrán látható. 1.7.
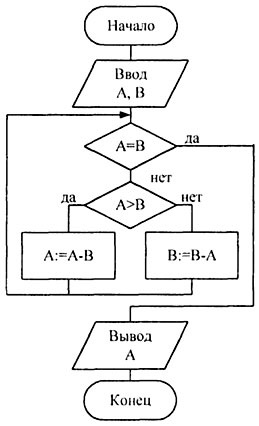
1.7 ábra - Példa folyamatábrák egyesített algoritmus
A folyamatábra mutatja részletesen összes funkcióját az algoritmus, de néha olyan nagy részletességgel nem teszi lehetővé, hogy azonosítsa a lényege az algoritmust. Ezekben az esetekben a leírás az algoritmus pszeudokódokra. A pszeudo-kód alapjául ugyanaz az alapvető struktúrákat, mint a blokkdiagramjait algoritmus (lásd 1.1.).
Példa 1.6.Opisanie euklideszi algoritmus pszeudokódokra.
1.1 táblázat - Példa pszeudokód feljegyzésére alap algoritmikus struktúrák
1.3. Feladatok rajz folyamatábrák
Egy egész szám m> 1.
Get a legkisebb egész szám k, így ahol a 4 k> m.
Adott egy n pozitív egész. Számoljuk ki a terméket.
Adott egy n pozitív egész.
N egész.
Szerezd meg a legkisebb számú formájában 2 r. meghaladó N (R - természetes szám).
Tekintettel a egész n, k (n k 0).
Adott egy pozitív egész szám, és n egy valós szám egy.
Adott egy n pozitív egész.
Adott egy n pozitív egész.
Összegét számolja ki az első n
Adott egy számsorozat. száma n - elemek száma a szekvenciában, és a számot x. Határozzuk meg az előfordulások számát az x érték egy előre megadott sorrendben.
Adott egy n pozitív egész. Számolja:
Mivel valós szám n természetes szám.
Adott egy számsorozat és n számú - elemek száma egy szekvenciában. Keresse meg a számos negatív eleme a sorozatban.
Mivel valós szám n természetes szám.
Let. Keresse yn első tagja. amelyekre az egyenlőtlenség. ahol - előre meghatározott valós pozitív szám.
Valós számok a és h, n szám.
Adott egy n pozitív egész. Számolja:
Adott egy számsorozat és n számú - elemek száma egy szekvenciában. Keresse meg az összeget a pozitív elemek a sorrendben.
Természetes N, X érvényes.
Adott egy számsorozat és n számú - elemek száma egy szekvenciában. Keresse meg a terméket a negatív elemeket a sorozat.
Mivel x valós szám, és n egész.
Számítani, anélkül, hogy a működését hatványozást.
Mivel x valós szám, és n egész.
Számolja. használata nélkül működésének hatványozást.
Adott egy n pozitív egész.
Valós számok x és egy természetes szám n.
Tegyük fel, hogy a számsorozat elő a következő törvény: = 1; ak = k * ak-1 + 1 / K; k = 1,2. N egész. Kap egy.
Adott egy n pozitív egész. Keresse meg a számjegyek száma a számát és összegét.
Let N- egész szám. Összegét számolja ki.
Adott egy x valós szám.
Pozitív egész n, m. Kap az m utolsó számjegye n.
Let N- egész szám. Összegét számolja ki.
Adott egy n pozitív egész.
Definiálja az algoritmus.
Sorolja alapvető tulajdonságait algoritmusok és bővítsék lényeg.
Besorolása szerint a típusú algoritmusok egy számítási folyamat?
Melyek a leírásának módjai az algoritmusok tudja?
Mit jelent a grafikai módon leírja az algoritmusok? Mi az előnye ennek a módszernek az a verbális leírása algoritmus?
Melyek az alapvető algoritmikus struktúrák és megindokolni.
Mi a célja az algoritmikus szerkezetek? Hogyan viszonyulnak az alapvető algoritmikus szerkezetek?