Faktorizációja - egy
Illusztráció polinom x 2 + cx + d = (x + a) (x + b), ahol a + b értéke egyenlő c, és a * b egyenlő d.
A matematika, faktorizáció vagy faktoring - bomlási egy tárgy (pl, a szám a polinomiális vagy mátrix.), Mint a termék más tárgyak, vagy faktorok. amely, ha megszorozzuk. így az eredeti objektumot. Például a 15. számú szorzott be prímszámokat 3 és 5, és a polinom x 2 - 4 szerepeljenek (x - 2) (x + 2). Ennek eredményeként a faktoring minden esetben a termék egyszerűbb tárgyak, mint az eredeti.
A cél az, hogy a faktorizációja az objektumot a „alapvető építőkövei”, például a k szám prímszámok, a polinom - az irreducibilis polinomok. Faktorizációja egész el van látva a a számelmélet alaptétele. és polinomok - algebra alaptétele.
Ennek az ellenkezője a Polinomok van kiterjedésük, többtagú szorzótényező megszerezni a „kiterjesztett” polinom írásbeli összegeként feltételeket.
Faktorizációja egész nagy számú feladat rendkívül összetett. Nincs ismert módszerrel megoldani ezt a problémát gyorsan. A komplexitás alapján néhány biztonsági algoritmusok nyílt kulcsú titkosítás. például RSA.
A mátrix is szorzott termékké mátrixok alkalmazások számára, ahol ez a forma kényelmes. Az egyik fő példa erre a használata ortogonális. és egységes háromszög alakú mátrixok. Vannak különböző módon, hogy a faktorizációt: QR-bomlás. LQ. QL. RQ. RZ.
Egy másik példa a tényezőkre funkciónak egy készítmény egyéb funkciók bizonyos tulajdonságú. Például, minden egyes funkció lehet tekinteni, mint egy készítmény szürjektıv injektıv funkciót. Ez a megközelítés általánosítása fogalmának faktorizációs rendszereket.
egészek
Az a számelmélet alaptétele, minden pozitív egész szám van egy egyedi prímfaktorizáció. Sok algoritmusok prímfelbontás, mely segítségével lehetőség van faktorizálni bármely pozitív szám akár a készítmény saját prímtényezője segítségével kiújulás képleteket. Ahhoz azonban, hogy igen nagyszámú hatékony algoritmust még nem ismert.
másodfokú polinomok
Bármilyen másodfokú polinom a komplex számok (polinomok a forma, ahol a ,, és ∈) lehessen venni típusú kifejezések segítségével a másodfokú egyenlet. Ez a módszer a következő:
ahol: és a két gyökerei a polinom talált másodfokú egyenlet megoldása.
Polinomok egészeken
Mindegyike binomiális egyenlő nulla az x és megtalálja a két gyökér. Faktoring ahhoz, hogy használni ezeket a képleteket, hogy megoldja a másodfokú egyenlet. Vegyük például 2x 2 - 5x + 2 = 0. Mivel a = 2 és Mn = a. Mn = 2, ami azt jelenti, hogy m és n értéke 1, és 2. Most van (2x + p) (x + q) = 0. Mivel c = 2, és PQ = c, PQ = 2, ami azt jelenti, hogy p és q értéke 1, és 2, vagy az egyik -1 és -2 a másik. Podstanovlyaya 1 és 2, vagy a -2 és -1 helyett p és q (Pn + mq = b), azt látjuk, hogy a 2x 2 - 5x + 2 = 0 szerepeljenek (2x - 1) (x - 2) = 0 így gyökerek X =
Megjegyzés: Snack eljárás annak meghatározására, hogy a második kifejezés pozitív vagy negatív (mint a fenti példában, az 1. és 2. vagy 1 és -2) áll annak ellenőrzésében a második tranzakciós trinomiális (+ vagy -). Ha van egy +, akkor ellenőrizze az első művelet, ha ő is + egy tagja számára pozitív lesz, és ha a művelet - a kifejezés negatív lesz. Ha a második művelet -, akkor az egyik tagja pozitív lesz, a második negatív. Egy ilyen ellenőrzés az egyetlen módja annak, hogy melyik elem lesz pozitív és néhány negatív.
Ha egy egész együtthatós polinom van diszkrimináns. ami egy tökéletes négyzet, akkor a polinom szorzott egészek.
Vegyük például egy polinomot 2x 2 + 2x - 12. Behelyettesítve az értékeket a másodfokú általános képletű, a diszkrimináns b 2 - 4ac 2 2 - 4 × 2 × -12 és 100. száma 100 egy tökéletes négyzet, így polinom 2x + 2 2x - 12 tényezőként egész számok; Ezek a tényezők egyenlő 2, (x - 2), és (x + 3).
Most tekintsünk egy olyan polinom x 2 + 93x - 2. A diszkrimináns 2 93-4 × 1 × (-2) egyenlő 8657, hogy nem egy tökéletes négyzet. Ezért, a kifejezés x 2 + 93x - 2 nem lehet tényezőként egészek.
Teljes négyzet trinomiális
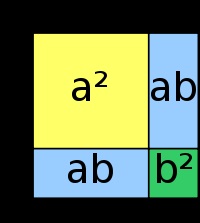
Illusztráció identitás (a + b) 2 = a 2 + 2ab + b 2
Néhány másodfokú egyenlet segítségünkre lehet két azonos binomials. Az ilyen egyenletek úgynevezett teljes négyzet trinomiális. Teljes négyzet trinomiális lehessen venni az alábbiak szerint:
Összeg / különbség a két négyzet
Egy másik gyakori módszer algebrai faktoring nevezik a különbség a két négyzet. Ez a használata az általános képletű
bármely két tagja, függetlenül attól, hogy tele vannak-e vagy sem a másodfokú egyenlet. Ha két szempontból vonnak le, akkor csak meg kell, hogy alkalmazza a képletet. Ha adunk, mind a binomiális, poluchinnye faktoring lesz képzeletbeli távon. Ez a képlet úgy reprezentálható, mint
Például lehetőség van arra, hogy számításba venni.
csoport
Egy másik módszer a faktorizációja néhány polinomok jelentése faktoring csoport. Azok számára, akik szeretnék fejleszteni az algoritmusok „faktoring csoport” lehet a legélvezetesebb megközelítés faktoring trinomiális mert szükség van a feltételezés az, ahogy a folyamat befejeződik.
Faktoring végzett csoportosításával helyen polinomiális tag két vagy több csoport, amelyek mindegyike lehet szorzott ismert módon. Az eredmények ezen factorizations néha kombinálható úgy, hogy egy egyszerűbb kifejezést. Például faktorizálni polinom
csoport a hasonló kifejezéseket:
és faktorizálni binomials
Ha szögletes trinomiális megvan a megoldás, hogy a racionális számok, találunk p és q, hogy pq = ac és p + q = b. (Ha a diszkrimináns négyzetszám, akkor létezik, különben mi lesz irracionális vagy komplex megoldások, és a feltételezés, racionális döntés érvénytelen.)
Top tagok közös tényező, hogy lehet használni, hogy megszabaduljon a nevező, ha nem egyenlő 1 Példaként tekintsük a másodfokú polinom
Ellenőrzése tényezők ac = 36 eredményük egy 4 + 9 = 13 = b.
más polinomok
Összeg / különbség a két kocka
Végezze faktoring összege és különbsége két kocka. Az összeget két kocka is képviselteti magát:
Például, x 3 - 10 3 (vagy x 3 - 1000) lehet tényezőként, mint: (X - 10) (x 2 + 10x + 100).
Lásd, amit a „Faktoring” más szótárak:
Faktorizációja - gráfelmélet, a bomlás a gráf diszjunkt élek átívelő részgráfját egy speciális fajtája. Általában van egy tényező átívelő részgráf egy adott tulajdonság. Egy példa az ilyen tulajdonság szabályszerűségének a gráf. Rendszeres ... ... Encyclopaedia of Mathematics
faktorizációja - Factorizing betartása és a Magyar helyesírási szótár ...
Lenstra faktorizáció segítségével elliptikus görbék - (Engl elliptikus görbe faktorizációs módszerrel, rövid ECM ..) Algoritmus faktoring egy természetes szám használatával elliptikus görbék. Ez az algoritmus van subexponential futás közben. A harmadik sebesség után ... ... Wikipedia
Faktorizáció segítségével elliptikus görbék - (Engl elliptikus görbe módszerrel, rövid ECM ..) Algoritmus faktoring egy természetes szám használatával elliptikus görbék. Ez az algoritmus van subexponential futás közben. Ez a harmadik sebesség után az általános ... ... Wikipedia
Faktorizációja egészek - faktorizációja természetes szám hívott annak felbontása a termék elsődleges tényező. A létezése és egyedisége (legfeljebb a sorrendben a tényezők), mint bomlás kell lennie a számelmélet alaptétele. Ezzel szemben a ... ... Wikipedia
Ekvivalencia reláció - Ebben a kifejezést, vannak más célra, lásd egyenértékűség .. A ekvivalencia arány () van beállítva, hogy egy bináris reláció, amely teljesíti a következő feltételeket: reflexivitás: minden egy. Szimmetria: ha ... Wikipedia
- Faktorizációja egészek. Dzhessi Rassel. Ez a könyv lesz összhangban a rendelését Technology Print-on-Demand technológiát. High Quality Content Wikipedia cikket! Faktorizációja? Teni egy természetes szám nevezzük ... Tovább Vásárlás 1125 rubelt
- Faktorizáció segítségével elliptikus görbék. Dzhessi Rassel. Ez a könyv lesz összhangban a rendelését Technology Print-on-Demand technológiát. High Quality Content Wikipedia cikket! Lenstra elliptikus görbe faktorizációs (Eng. ... Tovább Vásárlás 1125 rubelt
- Faktorizációs. Dzhessi Rassel. Ez a könyv lesz összhangban a rendelését Technology Print-on-Demand technológiát. High Quality Content Wikipedia cikket! ? A matematikában faktorizációt vagy F ktoring - ez ... Tovább Vásárlás 950 rubelt