Ellipszis, hiperbola, és parabola a szimmetriatengellyel párhuzamos a tengellyel


Az általános egyenlet II sorrendben görbe.
Ha az egyenleteket görbék: az ellipszis, hiperbola, és parabola, a szimmetriatengellyel párhuzamos tengelyek nyilvánosságra zárójelben, mindegyik lehet csökkenteni, hogy az öt-tagú egyenlet 2. érdekében, amely a formában:
Úgy hívják az általános egyenlet görbéjének 2. sorrendben.
Elemezve különbséget egymástól egyenletek formájában (1) az ellipszis, hiperbola, és parabola, akkor látható, hogy abban az esetben, egy ellipszis - jelek AiCodinakovy együtthatók esetében a hiperbola - koeffitsientovAiCrazlichny jelek, és abban az esetben a parabola egyik elérhető négyzetek jár egyenlőség nulla megfelelő koeffitsientaAiliC (odnovremennoAiCnulyu nem lehet egyenlő, különben a kapott egyenlet az 1. érdekében, azaz a közvetlen egyenletet).
Így a terméket ACopredelyaet görbe, melynek egyenlete a következő alakú (1).
Ellipszis AC> 0;
Mert túlzás AC<0;
A parabola AC = 0;
Nézzük meg az inverz probléma.
A Descartes-féle koordináta-rendszer a következő egyenlet adja:
A konstrukció a görbe és a teljes képet, hogy hogyan helyezkedik el egy síkban, szükséges ahhoz, hogy a (1) egyenlet egy kanonikus formában, vagyis azonosítani tökéletes négyzetek ebben az egyenletben.
Például, hogy az egyenlet kanonikus formában.
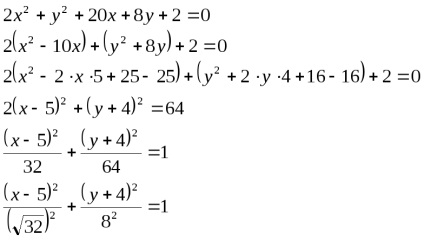
A derékszögű koordináta-rendszerben, az egyenlet 2. sorrendben:
, Meg tud felelni az alábbi hét típusú másodrendű vonalak. ellipszis, hiperbola, parabola, két metsző vonalak, pontok, egy pár párhuzamos vonalak, egy pár megfelelő sorokat.
Mi a pontok helye egyenlet által definiált
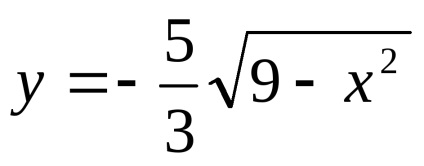
Mivel a jobb oldalon az egyenlet nem pozitív, akkor
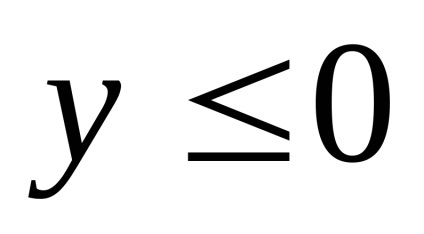
- a pontok halmaza egy ellipszis
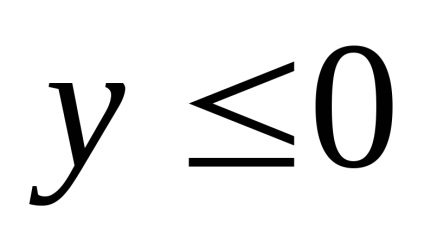


E szerint a egyenlet határozza meg, hogy milyen típusú görbe. Adj egy egyenlet kanonikus alakja, rajzoljon egy görbe a gépen XOY. Keresse meg a koordinátákat a foci. Tedd az egyenlet a aszimptotákkal a hiperbola:
Lásd. Táblázat (1). Mivel az egyenlet hiperbolikus görbét.
Itt az egyenlet kanonikus formában.
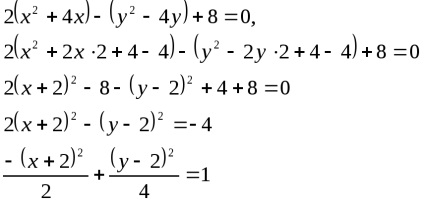
- kanonikus egyenlete hiperbola.
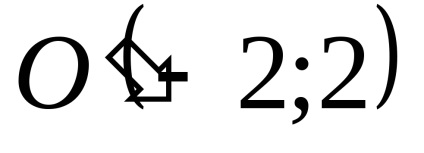

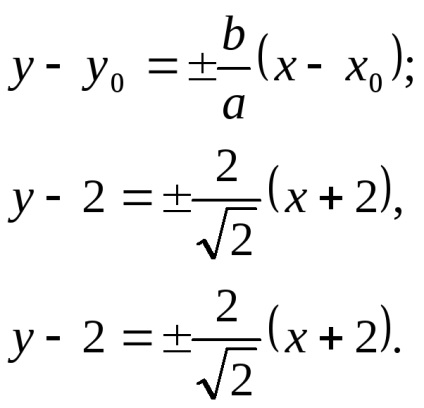
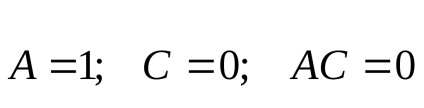
Mivel az egyenlet egy parabolikus görbe.
Itt az egyenlet kanonikus formában.
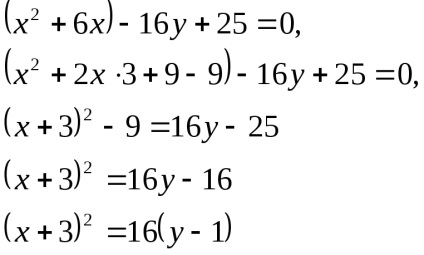
- kanonikus egyenlete parabola.
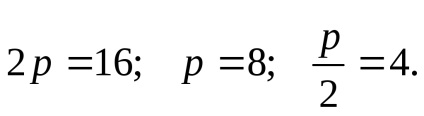
X = 0, akkor
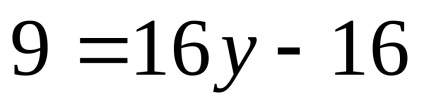
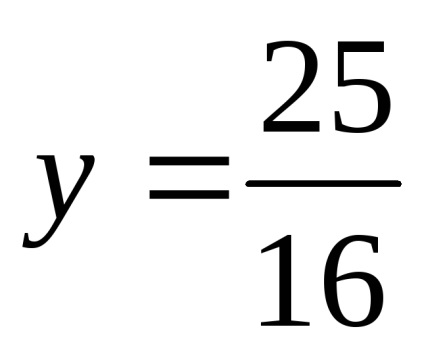
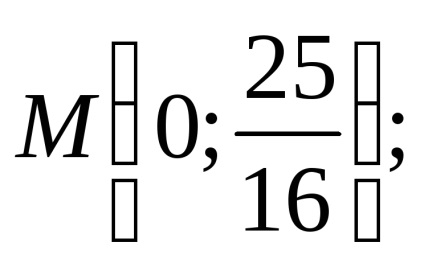


Mivel az egyenlet hiperbolikus típusú. Adunk el egy kanonikus formában.
Ez egy olyan eset a degeneráció a hiperbola 2 metsző vonalak:
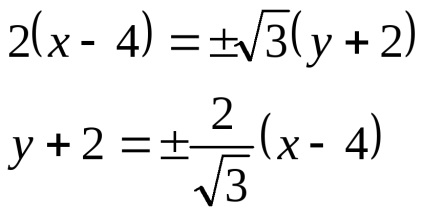
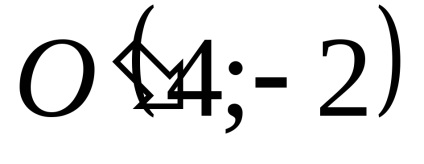
A lejtők egyenesek:
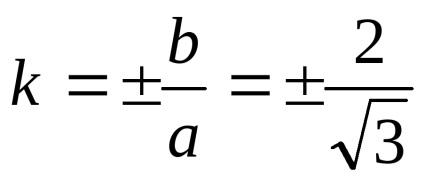
Jelenleg ezeket a sorokat:
Mivel az egyenlet az elliptikus görbe típusát.
A kanonikus formában.
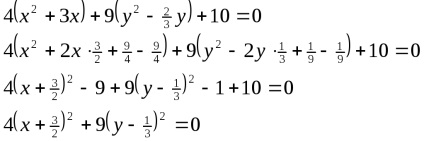
Ez egy olyan eset pontjában az ellipszis degeneráció
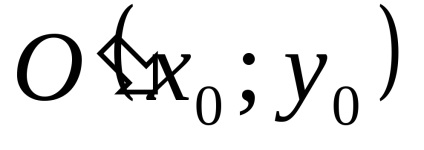
Ez teljesül, ha a koordinátái csak egy pontot:
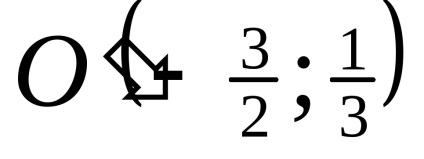

Construct egy görbe egyenlet által definiált
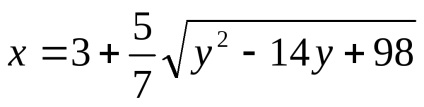
Ez az egyenlet egyenértékű a rendszer: vagy, következésképpen, az állapotban kapott egyenlet a hiperbola rész
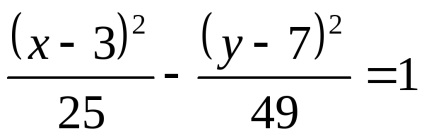
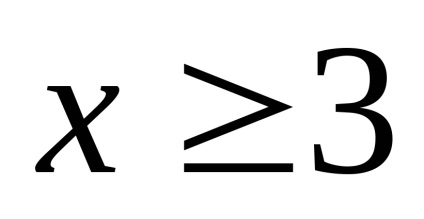
Építünk csak a jobb oldali ág a hiperbola, mint ez található a félsíkra ahol
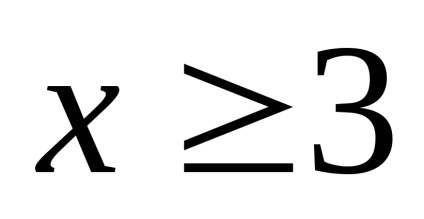


Construct egy görbe egyenlet által definiált
Ez az egyenlet egy görbe része, és ez felel meg a következő rendszerben:
Következésképpen, abban az állapotban, a következő egyenlet adja az ellipszis rész
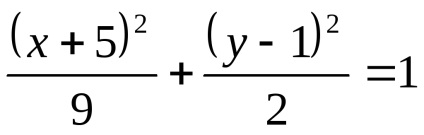
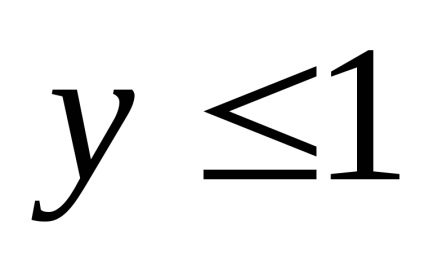


S. V. Frolov, R. Ya. Shostak, "Természetesen a magasabb matematika", Moszkva kiadó "High School" 1966.