Cyclomatic száma a gráf wiki
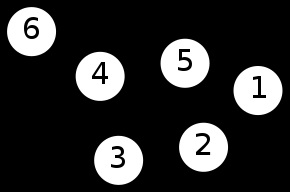
Ez a grafikon olyan körvonallal rang r = 2, mert lehet alakítani egy fa eltávolítását két él, mint a szélek 1-2 és 2-3, de csak egy eltávolítását éle elhagyja a hurok a grafikonon.
Gráfelmélet, a hurok rang [1] egy irányítatlan gráf - ez az élek minimális száma, amelyeknek eltávolítása tönkreteszi a ciklusban a gróf, fordult be egy fa vagy egy erdőben. Contour rangot úgy is lehet értelmezni, mint egy független ciklusok a grafikonon. Ezzel ellentétben, a megfelelő probléma találni egy sor ívek előre ciklusok [en], hogy irányított gráf. hurok rangot r könnyen kiszámítható a következő képlet
ahol m - az élek számát egy adott gráf, n - a csúcsok száma. és c - száma csatlakoztatott komponensek [2]. Az is lehetséges, hogy hatékonyan össze egy több bordát minimális mérete lebontó ciklusban egy mohó algoritmussal. vagy hozzáadásával feszítőfa.
Contour rangot is ismert, mint a cyclomatic száma a grafikonon. Meg lehet magyarázni szempontjából algebrai gráfelmélet a dimenzió ciklusos tér [en] a grafikon, tekintve matroidok fogalmait használva corank gráf matroidok [en] [3] szempontjából topológia és az egyik a számok Betty topologikus tér, amely származó a grafikon. Contour rang megszámolja a fülek a fülébe bomlása a grafikon, ami az alapja a koncepció paraméteres bonyolultsága [en] a fák, és szinte használt mutatók szoftver részeként meghatározó ciklomatikus komplexitás a kódrészlet. Című ciklomatikus komplexitás fogalmát vezette be Gustav Kirchhoff [4] [5].
Ligában Matroid előre és az épület egy minimális készlet ciklus [| ]
A kontúr a G gráf rangot lehet leírni az elmélet matroidok hogyan corank gráf Matroid [en], hogy G [6]. Figyelembe véve a tulajdonát matroidok kapzsiság, ami azt jelenti, hogy meg lehet találni a minimális élek, hogy tönkreteszi a ciklusban, a mohó algoritmus. kiválasztásával minden lépésben borda tartozó legalább egy ciklus a maradék gráf.
Másrészt, egy minimális készlet, amely elpusztítja az összes ciklus megtalálható megszerkesztésével feszítőfájának erdő G, és válassza ki a kiegészítő élek halmaza, amelyek nem tartoznak átívelő erdőben.
A független ciklus [| ]
Algebrai gráfelmélet. kontúr rang - a dimenziója gyűrűs tér [en] gráf Szemléletesen sem tudja megmagyarázni a vázlatot rangot a megszámoljuk a független ciklus a grafikon, ahol a készlet ciklusok tekinthető függetlennek, ha lehetetlen, hogy egy hurok, mint a szimmetrikus különbség egy részét a többi ciklus [2].
Ez a számítás független ciklusok is magyarázható a homológia elmélet. Topológia ága. Bármely G gráf lehet tekinteni, mint egy példa egy 1-dimenziós simplicial komplex. egyféle topologikus tér. által alkotott minden éle reprezentáció szegmens és kötést ezen szegmensek végein. A cyclomatic számát, az első helyezés (integer) a homológia a komplex [7]
Ezzel kapcsolatban, mint topológiai kapcsolási cyclomatic száma a G gráf is nevezik egy első számú Betty G gráf [8]. Általánosabban, az első Betti számát minden topologikus tér megszámolja független ciklusok az űrben.
Alkalmazások [| ]
kiépítés együttható [| ]
Opció kontúr rangot egy sík gráf. normalizálunk a lehető legnagyobb rangot bármilyen sík kontúr grafikon ugyanolyan csúcsok halmaza, az úgynevezett együttható kiépítés. A csatlakoztatott gráf sík szélei m és n csúcsú kiépítés együttható kiszámítható a következő képlettel [9]
Ebben a képletben, a számláló m # X2212; n + 1 általános képletben egy kontúr grafikon e rangot és a nevező a 2 n # X2212; 5 a legmagasabb lehetséges rangot síkbeli kontúr grafikon n csúcsú. reticulation faktor fekszik 0 és 1 között a fák maximális síkgráfok [en].
Fül bomlás [| ]
Contour helyezett számát tükrözi füle a fül bomlás a grafikon, a grafikon bomlása élek az út és kerékpárút, ami gyakran hasznos gráfalgoritmusok. Különösen a csúcsa a gráf 2-csatlakozását, ha és csak akkor, ha van egy nyitott fül bomlási sorrendje részgráfok ahol az első al-dobozok egy egyszerű ciklus, és a fennmaradó al-oszlopok egyszerű módon, és minden út kezdődik és fejeződik be a csúcsokat tartozó korábbi részgráfok, és minden belső csúcsa a pálya jelenik meg először ezen a módon. Mindenesetre összefüggő gráfok profilos rang r minden nyitott fül bomlás már pontosan r füle [10].
Szinte fák [| ]
Grafikont cyclomatic r szám az úgynevezett r is közel -fa. mert el akarja távolítani a grafikonon csak az élek r, hogy átalakítsuk azt egy fa vagy egy erdőben. Majdnem 1-tree szinte egy fa - a fa csatlakozik szinte psevdolesom. csenget a (lehetőleg triviális) fa gyökerezik minden egyes csomópontnál [11].
Általánosítás irányított gráfokra [| ]
Ciklikus rang [en] - ez invariáns orientált grafikonok. szintjének mérésével fészkelő ciklusok a grafikonon. Ez állandó bonyolultabb fogalom, mint cyclomatic helyezett (szorosan kapcsolódik a meghatározása a fa mélysége az irányítatlan gráfok), valamint a számítás sokkal bonyolultabb. A másik probléma az irányított gráfok kapcsolatos cyclomatic rang - meghatározása a minimális ív előre körök [en]. azaz a minimális ív, amelynek eltávolítási elpusztítja az összes irányított ciklus. Mindkét probléma, hogy a számítást ciklus rang és meghatározzuk a minimális készlet ívek rarezayuschiego ciklusok NP-nehéz.
Az is lehet számítani egy egyszerű invariáns orientált grafikonok, ha figyelmen kívül hagyja az irányokat élek, és kiszámítja a rangot gyűrűs irányítatlan gráf. Ez az elv az alapja meghatározásának ciklomatikus komplexitás. méri összetettsége miatt a számítógépes program értékelésére összetettsége számítógép kódrészlet.
Kapcsolódó fogalmak [| ]
Egyéb számok definiálható eltávolítását szélei irányítatlan gráf tartalmazza a borda kapcsolatot. Az élek minimális száma, amelynek eltávolítása elvesztéséhez vezet a kapcsolat és a számát a megelőzés párosıtások [en]. Az élek minimális száma, amelynek eltávolítása elvesztéséhez vezet, hogy létezik egy teljes párosítás.