bemutatása a piramis
2. Mi a Piramis Piramis - mértani alakzat, amely egy sokszög, a lényeg nem síkjában a sokszög és minden összekötő szakaszok ebben a kérdésben, hogy a poligon pont.

3 piramis apothem magassága oldalfelületeinek rendszeres piramis levonni annak csúcsait; oldalfelületei háromszögek konvergáló a csúcsnál; oldalirányú bordák közös oldalán oldalfelületek; piramis vertex pont, összekötő oldalsó élek és fekvő bázis síkban; a magassága a merőleges szegmens átszívott a piramis vertex, hogy az alap síkjában (a végei ebben a szegmensben a piramis csúcspont és a felületi normális); átlós részének a piramis a piramis szakasz, amely átmegy a felső és az alap az átló; bázis sokszög, amely nem tartozik a csúcsa a piramis.

4
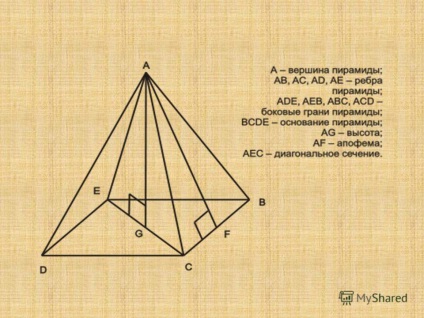
6. Helyes Piramis Piramis úgynevezett reguláris, ha az alap egy szabályos sokszög és vertex kivetített közepén a bázis. oldalsó szélei a piramis jobb; a jobb oldalon arcok a piramis minden egyenlő szárú háromszögek; minden rendszeres piramis egyaránt levelet, és leírja a hatálya körülötte; jobb oldali felülete a piramis fele a termék a kerülete a bázis apofemu. Tulajdonságok rendszeres piramis.

7 Egy téglalap alakú piramis piramis nevezett négyszögletes, ha az egyik oldalsó szélei a piramis merőleges az alapra. Ebben az esetben ez a szélén és magassága a piramis.
8 csonka gúla csonkagúla nevezzük poliéder, zárt között az alapja a piramis és egy szelő párhuzamos síkban az aljához.
9 Tulajdonságok piramisok Ha minden oldalsó szélei egyenlő, akkor: alján a piramis lehet leírni, mint egy kör, a tetején a piramis az előrejelzések a közepén; oldalirányú bordák a alapsík azonos szögtávolságban. Ennek a fordítottja is igaz, azaz ha az oldalélek egy olyan bázist képezzenek síkban azonos szögben, vagy ha közel az alján a piramis lehet leírni, mint egy kör, a tetején a piramis az előrejelzések a közepén is, akkor az összes oldalélei a piramis egyenlő. Ha az oldalsó felületek vannak döntve, hogy a gép a bázis egy adott szögben, akkor: az alapja a piramis, akkor helyezni egy kört, a tetején a piramis az előrejelzések a közepén; a magassága a oldalfelületek egyenlő; oldalán felülete felével egyenlő az alap kerületét termék magassága az oldalsó felület.
10 Tétel Tétel Ha az oldalfelületeket a piramis egyformán hajlanak arra a síkra, a bázis és kiterjeszti a magassága a piramis, a magassága közepén halad át a beírt kör a bázis a piramis. Tétel Ha minden az oldalsó felületek vannak döntve, hogy az alap sík ugyanolyan szögben, hogy ez a képlet érvényes elsősorban rendszeres piramis.
11 képletű társított piramis piramis Volume lehet képlettel számítottuk ki: ahol S lábnyom és magassága; ahol h a kötet a doboz; Továbbá, a hangerőt a háromszög alakú piramis (Tetrahedron) lehet kiszámítani a következő képlet szerint. Amennyiben ferde bordák, térköz és a szög között és; Az összeg a teljes felülete az oldalsó felülete és a bázis közelében meghatározásához oldalsó felületén egy egyenes gúla használhatja a képlet:
12. Példák a problémamegoldás adott. Szabályos négyszögletes gúla SABCD bázis középpontja O, S vertex, SO = 51, AC = 136. Talált: oldaléle SC. Megoldás: SOC: rectangel, SOC szög = 90 °
13 Adott: Szabályos háromszög piramis SABC R közepén borda BC, S csúcs. Ismeretes, hogy az AB = 7 és SR = 16. Talált: palástfelületén. Megoldás: 1) területe oldalfelületének egy szabályos háromszög alakú piramis felével egyenlő a termék a bázis kerülete a apofemu (apothem a magassága oldallapja egy szabályos piramis végzett annak csúcsa): 2), vagy lehet mondani, hogy az oldalsó felülete a piramis az összege területek három oldalfelülete. Az oldalsó élek egy szabályos háromoldalú piramis egyenlő területű háromszöget. Ebben az esetben: