az integrátor
Behelyettesítve egyenlet (1,63) értékei B0 = ia0 0 = A2 = 0. Kapunk egy állami egyenletet az alábbi formában (elsőrendű differenciálegyenlet):
Kimeneti paraméter szinten arányos a szerves annak bemeneti paraméter, és írja le a következő kifejezés:

Az átviteli függvény integrálja kapcsolatot kell találni a Laplace transzformáció lesz a következő formában:

Ebben az esetben k - a relatív átviteli kapcsolat, amelynek itt a mérete határozza meg a dimenzió aránya a változás mértéke a kimeneti paraméter a bemeneti dimenzió.
Átmeneti Link funkció X (t) = 1 (t) az alábbi ábrázolás:

Ebben az esetben, a C - egy integrációs konstans, a kezdeti feltételeket nullával egyenlő.
Az állandó kimeneti paraméter visszajelzést bemeneti paramétere változtatható lehet, mint állandó integráció különféle értékeket vehet fel azzal kapcsolatban integráló egység nevezett sarkítatlan. Ha az érték a bemeneti paraméter
nullára csökken, szemben az arányos nyereség, az integrálódó kapcsolati paraméter értéke a kimenet nem általában nulla.
Az integrátor is nevezik integrátor. A APFC integrátor szubsztituált expressziós (1,70.) Jw helyett p, és azt kapjuk:

A kifejezést azt mutatja, hogy a tényleges frekvencia jellemző Re (w) egyenlő nullával, a képzeletbeli frekvencia karakterisztika egybeesik a frekvencia:

Következő, azt látjuk, a PFC integrátor az alábbiak szerint:

Ebből az következik, hogy az integrátor csillapítja a magas frekvenciák és korlátlan növeli az alacsony frekvenciákat. Az amplitúdó a kimeneti hullámforma nulyus általában növeli a frekvenciáját a bemeneti rezgések, míg a fáziseltolás állandó, és egyenlő - π / 2.
Grafikus ábrázolás szintű jellemzőket a 30. ábrán látható.
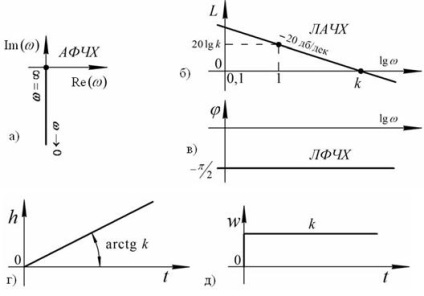
Ábra30. Jellemzői integrálása a) komponenst, b), c) - frekvencia;
Meglévő valódi integráló egység characterized''nakaplivaniem 'bemeneti akció és birtokában értékelhető in ?? ertsionnostyu.
Az integrátor nem lehet egyensúlyi bármilyen konstans értéke a bemeneti jel.
Befolyása alatt azt a legkisebb értéket a bemeneti paraméter kimeneti paraméter értéke neĸᴏᴛᴏᴩᴏᴇ idővel válhat
aránytalanul nagy. Az egyensúlyi helyzet a link csak akkor érhető el, ha nincs bemeneti akció.
Példák létező egységek a kondenzátor szolgálhat egy (elektromos kapacitás), egy hidraulikus lengéscsillapító, stb Vezetési igazi ötlet integrátor a 31. ábrán látható.

Ábra31. A tényleges ábrázolása integrátor (kondenzátor)
lásd még
Az integrátor - egységnyi melynek kimenete arányos az idő elválaszthatatlan a bemeneti nagyságát. 1,53 1,54 ahol k - arányossági tényező megadott linkre. A változás sebessége kiadási nagyságát integrátor, arányos a bemeneti. [További információ].
Az átviteli függvény: W (p) = k / p. Tekintsük a speciális esetben, amikor a k = 1, azaz a W (p) = 1 / p. APFC: W (j . [További információ].
Differenciálegyenlet kapcsolat általában írt ki az alábbi űrlapot. (3,44), ahol K1 - dimenziós mennyiség, mint az (3,36). Ha hvyh (t) és x € X (t) azonos dimenziót, a dimenziója k1 értéke 1 / p. Ezután (3,44) úgy reprezentálható, mint. (3,45), ahol; - időállandó. [További információ].
Dynamics, amely a folyamat egy egység a következő egyenlettel. ahol k - erősítés. 1. Átmeneti válasz: 2. Az impulzusválasz: 3. Az átviteli függvénye egy igazi integrátor: Real integráció link. [További információ].
Differenciálegyenlet kapcsolat általában írt ki az alábbi űrlapot. (3,44), ahol K1 - dimenziós mennyiség, mint az (3,36). Ha hvyh (t) és x € X (t) azonos dimenziót, a dimenziója k1 értéke 1 / p. Ezután (3,44) úgy reprezentálható, mint. (3,45), ahol; - időállandó. [További információ].
Dynamics, amely a folyamat egy egység a következő egyenlettel. ahol k - erősítés. 1. Átmeneti válasz: 2. Az impulzusválasz: 3. Az átviteli függvénye egy igazi integrátor: Real integráció link. [További információ].
Építőipari végezzük az alábbi képlet szerint. Az adott értékek a k és T. Azáltal w = 0; 10; 20; 30; 50; . [További információ].
Építőipari végezzük az alábbi képlet szerint. Az adott értékek a k és T. Azáltal w = 0; 10; 20; 30; 50; . [További információ].
További tehetetlenségi elem neve - aperiodikus eleme az elsőrendű. Által leírt differenciálegyenlet (3.3) ahol T - az idő állandó szintre, k - erősítés. Az üzemeltető egyenlet (Tp + 1) Y (p) = kx (p). Amikor az átviteli függvény p = 0. [tovább].
További tehetetlenségi elem neve - aperiodikus eleme az elsőrendű. Által leírt differenciálegyenlet (3.3) ahol T - az idő állandó szintre, k - erősítés. Az üzemeltető egyenlet (Tp + 1) Y (p) = kx (p). Amikor az átviteli függvény p = 0. [tovább].