Az a képesség, hogy mozogni lesz az úgynevezett egy pont egy anyagi rendszer végtelenül kis elmozdulás,
Előadás 8. virtuális munka és az általános egyenlet dinamikáját.
Ez az előadás a következő témákat:
1. Lehetséges elmozdulás. Osztályozása kötvények.
2. A virtuális munka pénzügyi egyensúly a rendszer. Az általános egyenlete statika.
3. virtuális munka a mozgás egy anyagi rendszer. Az általános egyenlete dinamika
4. Az általánosított koordinátákat.
5. általánosított erők.
6. Lagrange egyenletek egyensúlyt.
7. általánosított tehetetlenségi erő.
8. Lagrange egyenletek.
A tanulmány ezeket a kérdéseket szükséges a tanulmány a csappantyú a fegyelem „Alkatrészek”, hogy megoldja a problémákat, a tudományok „Theory of Gépek és mechanizmusok” és a „Strength of Materials”.
Lehetséges mozgás. Osztályozása kötvények.
Tanulmányozása során egyensúlyi szervek úgynevezett geometriai statikus egyensúlyi kell vizsgálni az egyes szervek külön-külön, felváltva az egyes kommunikációs egymásra előzőleg ismeretlen reakciókat. Ha a szervezetek számát egy nagy rendszer, így ez lesz nagyon nehézkes, és a kapcsolódó meg kell oldani a nagy számú egyenletek sok az ismeretlen.
A megkülönböztető jegye a módszer eredő virtuális munka az a tény, hogy annak alkalmazása a hatása a linkek nem veszik figyelembe bevezetésével ismeretlen előzetesen reakciók, valamint figyelembe vesszük a mozgások, akkor lehet mondani a rendszer pont, ha levezetni a rendszer abból a helyzetből, hogy elfoglalja. Ezeket a mozgásokat hívják mechanika vozmozhnymiperemescheniyami.
Tekintsük a lehetséges elmozdulását az M pont a rúd rögzítve a rögzített felület a D csukló (2a ábra). Persze, a bár nem engedi, hogy egy pontot a gömbfelület bármely irányban, és bármilyen távolságra. Mindezek a mozgalmak lehetséges. Talán, az úton, a mozgó és lefelé. De ez a mozgás nem nevezhető lehetséges, mert a törött rúd.
Ezen túlmenően, a képesség, hogy mozgatni csak akkor úgynevezett kis elmozdulás, mint egy kis része a pálya, hogy lehet helyettesíteni egy egyenes pályaszakasz érintőleges.
Most már megfogalmazni meghatározásának lehetséges mozgását.
Az a képesség, hogy mozog a pont az anyag rendszer lesz az úgynevezett infinitezimális mozgása megengedett a megszorítások a rendszer.
Az a képesség, hogy mozog egy pontrendszer két feltételt kell teljesítenie:
1) kell lenniük végtelenül kicsi, mivel a rendszer fog mozogni, hogy egy másik helyzetbe, ahol az egyensúlyi feltételek különbözőek lehetnek alatt véges elmozdulások;
2) kell lennie, hogy az összes kivetett megszorítások a rendszer fenntartása, mert különben meg fog változni a véleménye a helység mechanikai rendszer (sistemastanet egyéb).
Például, a forgattyús mechanizmus az 1. ábrán látható a mozgás pontok OA hajtókar helyzetét OA1 nem tekinthetők lehetséges, mivel ebben a helyzetben a mechanizmus, egyensúlyi körülmények között, és erők más lesz. Hasonlóképpen, nem kell figyelembe venni is lehetséges infinitezimális egy pont elmozdulását alkalmazzuk az a rúd a vonal mentén BD; lenne lehetséges, ha a B pont helyett a csúszka lenne forgókuplunggal, azaz amikor a mechanizmus más lenne.
Így a lehetséges elmozdulás a rendszer nevezünk minden olyan halmaza végtelenül elmozdulás pont a rendszer megengedett pillanatában minden megszorításoknak a rendszer. Lehetséges mozgása bármely pontján jelenik meg a rendszer által képviselt elemi vektor. felé elmozdulás.
Általában a pontokat és telefon rendszer lehet, hogy sok különböző lehetséges elmozdulások (elmozdulások és nem tartjuk más). Azonban minden rendszer jellegétől függően a kapcsolatok rá rótt, megadhat egy bizonyos számú, egymástól független mozgások, esetleges egyéb mozgást fog kapni, mint a geometriai összege. Például egy labda feküdt néhány sík (vagy felület), lehet mozgatni síkja mentén több irányban. Azonban az esetleges mozgást lehet beszerezni, mint az összeg két mozgások mellett, valamint síkjában fekvő merőleges tengely ().
A független egymás között, lehetséges elmozdulásai az rendszer az úgynevezett számát szabadsági fok a sistemy.Tak fent tárgyalt gyöngy egy síkban (vagy felülete), ha úgy tekintjük, mint egy anyagi pont két szabadsági fok. A forgattyús mechanizmus nyilvánvalóan fokú szabadságot.
A szabad anyagi pont - 3 szabadsági fok (független 3 mozognak egymásra merőleges tengely). Szabad merev test hat szabadsági fok (független mozgások 3 transzlációs mozgás három tengelyén és a forgási körül ezek a tengelyek).
Ehhez hozzá kell tennünk néhány megjegyzést.
Először. A neve E mozgalmak azt mutatja, hogy ezek csak akkor lehetséges, de nem kötelező; hogy ezek a mozgalmak egy adott helyzetben a rendszer lehet, hogy sok; hogy közülük csak egy érvényes (Ha a kommunikáció - nem rögzített, változik az idő múlásával, a tényleges mozgás nem lehet az egyik lehetséges); hogy ezek a mozgalmak nem fordulnak hatása alatt ható erők a rendszert, és, hogy úgy mondjam, kérésünkre.
Második. Mivel a kis mérete az ilyen mozgások mentén vannak érintő a röppálya és így, az irányba, hogy egybeesik a sebességvektor. Ez a sebesség ebben az esetben is nevezik sebességet teszi lehetővé. nem érvényes.
Harmadik. Ha vannak linkek között a pontok között anyagi rendszer, a lehető elmozdulása ezek a pontok egymáshoz való függőség megállapítása kényszer egyenletek.
A 2. ábra néhány példát ad a lehetséges elmozdulásai pontok néhány anyagot rendszerek.
Ezekből a példákból az következik, hogy az egyetlen lehetséges mozgás a test forgási tengelye körül, egy kis forgatás szögét. És az esetleges elmozdulások a pontokat lehet meghatározni a segítségével ez a szög. Így például, (ábra a 2a és 2b).
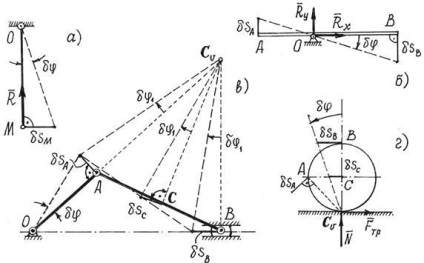
Mivel az irányok mozgások lehető legnagyobb sebességgel irányba, a mozgás a link mutat AB (ris.64, c) segítségével határozzuk meg a pillanatnyi közepén ezt a linket sebességgel. Egy lehetséges mozgását a teljes test síkkal párhuzamos mozgás - a forgás egy kisebb szögben tengely körül közepén áthaladó pillanatnyi sebesség. Ez a szög lehet meghatározni.
Ettől. akkor. és csúszka mozgó pont W. S .. Azaz, a elmozdulások minden pont a mechanizmus lehet meghatározni egy lehetséges mozgás, a mozgás OA ellátás. szöggel.
Hasonlóképpen, a forgatás egy kis szög körüli pillanatnyi központjában sebességek. azonosítja lehetséges mozgását a kerék pontot, amely csúszásmentesen gördülni mentén rögzített egyenes vonal (2. ábra, g).
A munka a ható erők a pénzügyi rendszer lehetséges mozgásának hívjuk fel a munkaképességét.
Ha megnézzük a különböző anyagi rendszerek, előfordulhat, hogy az elemi munka a reakciók sok linkeket virtuális elmozdulás lesz nullával egyenlő. Az ilyen kötések, az összeg a lehetséges reakciók, amely működik esetleges mozgása nulla, az úgynevezett ideális korlátok. Ilyen kötőanyagok közé tartoznak például, az összes kapcsolatot súrlódás nélkül.
Communications, amik nem változnak az idővel hívják helyhez.
Vannak linkek nevezzük, illetve visszatartás vagy egyoldalú, attól függően, hogy akadályozzák a mozgás a lényeg ellentétes irányban, vagy csak egy.
Bizonyos anyagi rendszerek is vannak egészen komplex kapcsolatok, amelyek korlátozzák, vagy csak a helyzet a rendszer, a koordinátáit vagy több pontot, és arányuk származó idő koordinátákat. Az első az úgynevezett holonomic, geometriai, kapcsolatokat; második - holonomic, filmszerű, nem integrálható. Mi ezentúl úgy csak rendszerek holonomic korlátok.