Általános jellemzői elosztási probléma
Distribution kapcsolatos feladatokat a források elosztása a munkát, amit meg kell tenni. Az ebbe az osztályba problémák merülnek fel, ha a rendelkezésre álló források nem elegendőek, hogy végre minden művelet a leghatékonyabb módon. Ezért a cél a probléma megoldásának az, hogy megtaláljuk az ilyen forgalmazási a forrás, amelyben vagy minimalizálja a teljes költséget az munkavégzés vagy maximalizált származó teljes bevétel.
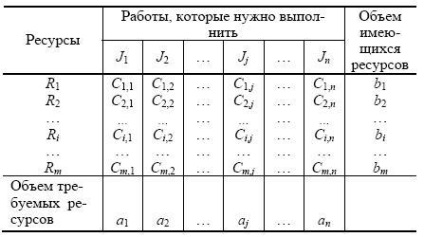
A legtöbb feladatot is képviselteti magát a forgalmazási forma a mátrix táblázatban szereplő 5.1.
Elements Cij. állt a sejtekben a mátrix, a kapcsolódó költségeket vagy a jövedelem megfelelő elosztásának egy erőforrás egységben Ri munkát Jj. Az értékek Cij lehet független és függő.
Például eredő költségek kinevezését a gépjármű egy bizonyos útvonalon áruszállítás, nem attól függ, milyen gépeket rendelt más útvonalakon szolgáltatást. Ugyanakkor az értékesítési osztály (például a termelési) általában attól függ, mi az alapokat költöttek más részlegek (pl Sales). Az elosztó elmélet középpontjában főként a feladatok független költség és bevétel. Ez azzal magyarázható, nem pedig az a tény, hogy az ilyen feladatok sokkal fontosabbak, hanem csak azokra, amelyek sokkal könnyebb építeni egy modellt, és kap megoldásokat.
Ha a költség (vagy haszon) meghatározott térfogatú erőforrás Hij I, Ji kiválasztott munka elvégzésére HijCij egyenlőek, akkor van egy lineáris elosztási probléma.
Alapvető megoldási módjait, disztribúciós problémák, különösen a lineáris programozás, arra a feltételezésre épülnek, hogy a hangerő a rendelkezésre álló erőforrások (bi) a szükséges mennyiségű (aj) és a költségek (Ci, j) pontosan ismertek.
Ha a teljes mennyiség a rendelkezésre álló források # 931; bi (i = 1 ... m) egyenlő a teljes kereslet a számukra # 931; aj (i = 1 ... n), akkor van egy kiegyensúlyozott (zárt) elosztási probléma. Ha azonban # 931; aj ≠ # 931; bi. akkor a probléma az úgynevezett aszimmetrikus (nyitott). Ha a forrásokat lehet osztani a munkahelyek között, néhány munkát lehet végezni, ha különböző kombinációi források. Ha a munka és a forrásokat egységekben mérjük az azonos méretű, ezek a problémák általában a továbbiakban a szállítás vagy a feladat bomlás. Ha a munka és a források más egységekben, akkor a probléma az úgynevezett általános elválasztási feladat. Így a közlekedési probléma egy konkrét esetben az általános elosztási probléma.
Módszerek működési
Van néhány M szállítókra. Az összeg az áruk között szállít az A1. A2, ..., am egység. Vannak N fogyasztók ezen árucikk; a kereslet B1. B2. ..., BN egység. A készletek áru rendelkezésre bocsátását, az összegével egyenlő a kereslet minden fogyasztó:
Ismert az egység szállítás költsége minden szállító minden egyes vevő (szállítási költség): Cij. i = 1, ..., M, J = 1, ..., N.
Ez szükséges ahhoz, hogy a szállítási tervet (hogyan, hol és hány egység fel), hogy minden alkalmazás tettek, és az összesített értéke volt a forgalom minimális.
Nézzük először a megoldás a közlekedési problémát zárva van, azaz, ha az összeg az összes ajánlatokat egyenlő az összeg az összes tartalék.
Magyarázza meg a legegyszerűbb módja az lenne, egy konkrét példát:
Példa 5.1. Négy raktárak (CK1S, CK2, CK3, ck4) Szállításait a három üzlet (mg 1, mG2 MG3). Raktáron TC1 40 tonna áru raktáron CK2 - 50 tonna készleten TC3 - 60 tonna készlet ck4 - 30 tonna. Store mg 1 szükséges 60 tonna áru, áruház MG2 - 80 tonna, bolt MG3 - 40 tonna. A költségek (a dolgozószobában. U), kapcsolódó szállítása egy tonna áru egyes raktár minden boltban, táblázatban mutatjuk be. 5.2.
Ez szükséges annak megállapítására, hogy milyen sok a szállítandó áru egyes raktárban minden boltba szállít a boltok szükséges mennyiségű áru minimális költségekkel.
Ez a probléma is képviselteti magát, mint egy lineáris programozási feladat. A konstrukció egy matematikai modell ezt a problémát, bemutatjuk változók xij. i = 1, ..., 4, J = 1, ..., 3, jelezve a szállított áruk a i-edik raktárból a j-edik tárolni.
A raktárak 180 egység áruk; 180 is tárolja szükséges áruk egység. Ezért, hogy a kereslet kielégítésére minden üzletben kell kivenni az árut a raktárak az egész. Korlátozások kifejező ez a követelmény a következő:
Minden áruház kell szerezni annyi terméket amire szüksége van. Korlátozások kifejező ez a feltétel a következő:
Mivel a változók számát jelzik a szállított áruk, rájuk nem negativitás követelmény:
A célfüggvény a költsége megfelel az összes forgalom:
Ezt a problémát meg lehet oldani a szimplex módszer, valamint bármely lineáris programozási feladat. Azonban ez a megoldás meglehetősen bonyolult, mivel a nagyszámú változót és korlátok szerepelnek a matematikai modellben a probléma. Ahhoz, hogy a problémák megoldása az ilyen jellegű, vannak speciális, egyszerűbb módszerekkel.
Megoldásában a közlekedési problémát a használata kényelmes, a számítási táblázat tartalmazza a szállítás költségét, áruk készletek beszállítóktól és értékét a fogyasztói kereslet. Ennek során a probléma megoldásának annak rögzített értékének szállítmányok (változók értékei xij), valamint a kiegészítő értékeket használnak, hogy megoldja a problémát. Számítás például asztalra 5.1 táblázatban mutatjuk be 5.3.