Általában elutasítja a null és alternatív hipotézist határozat

Ha empirikus kritérium értéke egyenlő a kritikus értéket, amely megfelel a £ 0,05, vagy nagyobb, mint, majd H0 elutasítják, de még nem tudjuk biztosan fogadja H1.

Ha empirikus kritérium értéke egyenlő a kritikus értéket, amely megfelel a £ 0,01, vagy azt meghaladja, H0 utasítani és elfogadott H1.

Kivételek G. előjel próba és Wilcoxon T Tesztkritérium Mann-Whitney U. Számukra állítsa vissza a kapcsolatot.

Hogy megkönnyítse a döntéshozatali folyamat lehet minden alkalommal plot „jelentőségét tengely”:

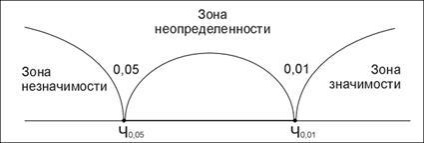
„Axis jelentősége” egy egyenes vonal a bal végén, amely 0, bár általában nem figyelhető meg a cél vonal, balról jobbra, és növekszik a számsorok. Valójában ez a szokásos iskolai abszcissza OX derékszögű koordináta rendszerben. Azonban a jellemzője ennek a tengely, hogy három helyen választott, a „zóna”. A bal oldali terület az úgynevezett „zóna jelentéktelenség”, ugye - „fontos a terület”, és a köztes - a „zóna a bizonytalanság.” A határokat a három terület a kritikus értéket, amely megfelel a £ 0,05 (jelöljük CH0,05), és a kritikus értéket, amely megfelel a £ 0,01 (jelöljük CH0,05).

Már a kritikus értéket CH0,01 kiterjeszti „terület jelentőségét” - itt jönnek a tapasztalati értékeket meghaladó CH0,01. és ezért jelentős. Ebben az esetben elfogadta az alternatív hipotézis H1:

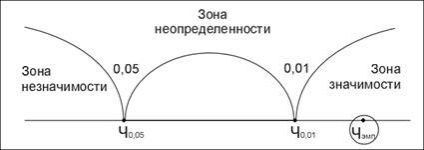
A bal oldalon a kritikus értéket CH0,05 húzódik „jelentéktelenség zóna” - ide tartoznak az empirikus értékek kotoryenizhe CH0,05 ezért elhanyagolható, és ebben az esetben azt a hipotézist, H0 nincs különbség:

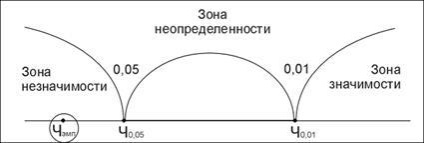
Ha tapasztalati érték alá esik „zóna a bizonytalanság.” elutasította azt a feltevést, megbízhatatlansága különbségek (H0), de a hitelesség hipotézis (H1) nem került elfogadásra:

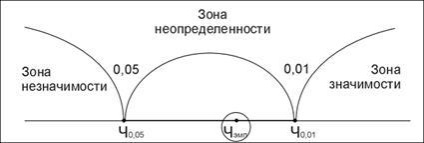
A gyakorlatban azonban, a kutató már jelentősnek tekinthető e különbségek, amelyek az „zónájában bizonytalanság”, amely megállapítja, hogy azok jelentősek egy £ 0,05, illetve megadásával pontos szignifikancia szintjét chennogo szemi-empirikus kritérium értéket, például: a = 0, 02.

A statisztikai szignifikancia szintjét vagy kritikus fontosságú meghatározott kritériumok eltérő módon, miközben ellenőrzi irányított és nem irányított statisztikai hipotéziseket.

Amikor az irány statisztikai hipotéziseket használt egyoldalú kritérium nem irányított hipotézis - kétoldalas tesztet. Kétoldalú szigorúbb feltételt, mivel azt ellenőrzi a különbség mindkét oldalon, úgy, hogy a tapasztalati érték a kritérium, amely megfelel a szignifikancia szintet, mielőtt a £ 0,05, csak most megfelel arra a szintre, a £ 0,10.

Hagyja, hogy a kritikus értékek a Q 6 és 9and -Rozenbauma kritérium rendre jelöljük Q0,05 = 7 és Q0,01 = 9. Elfogadta az alábbi formanyomtatvány a kritikus értékek:

Tegyük fel, hogy az empirikus kritérium értéke egyenlő 8: Qemp = 8. A „tengelyen a fontosságát” tapasztalati érték zárt ellipszis:

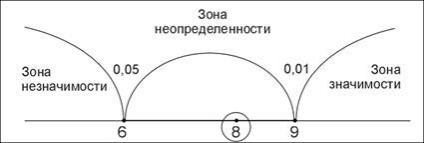
Empirikus kritérium értéke a probléma abban rejlik közötti régióban Q0,05 és Q0,01. és akkor feltételezhetjük, hogy a különbségek szignifikánsak £ 0,05.

Power a teszt - az a képessége, hogy azonosítsa a különbségek, ha van ilyen. Más szóval, az a képessége, hogy utasítsa el a nullhipotézist nincs különbség, ha ez nem megfelelő.

A hiba abból áll, hogy elfogadjuk a nullhipotézist, miközben ez nem igaz, az úgynevezett II-es típusú hiba.

Annak valószínűsége, hogy egy ilyen hiba nevezzük b. Teljesítmény Kréta-dence - az a képessége, hogy megakadályozza a másodfajú hiba, így a teljesítmény 1- b.

Teljesítmény kritériumot empirikusan. Ugyanez a probléma is megoldható különböző feltételek: ha úgy találja, hogy egyes kritériumok mutatják az idő különbség, ahol mások nem teszik meg, vagy ha egy magasabb szintű szignifikáns különbségek. Felmerül a kérdés: miért, akkor, hogy egy kevésbé erős teszteket? Az a tény, hogy az alapján a kiválasztási kritériumok lehet nem csak a hatalom, hanem egyéb jellemzők, mégpedig az egyszerűség, a szélesebb körű használatát, alkalmazhatóság vonatkozásában az egyenlőtlen minta mérete, leginkább informatív eredményt.

? Kérdések és Gyakorlatok

5. Határozza meg a következő fogalmakat:

§ null és alternatív hipotézisek;

§ hiba az első fajta, a hiba a második fajta;

§ a statisztikailag szignifikáns szintet;

2. Ismertesse a parametrikus és nem parametrikus módszerekkel.

3. Játssz a jogot, hogy elvetjük a nullhipotézist, vagy alternatív döntést.

4. A kritikus értékek c 2 (Pearson-teszt) statisztikai táblázatok rendre:

Ennek alapján a kritikus értékeket adja határozat (válassza ki a megfelelő hipotézis - H0 vagy H1), hogy a következő empirikus értékek: