A terület egy paralelogramma, háromszög és trapéz
Meg kell határozni, mi az a magasság, a paralelogramma.
Ez merőleges által végzett bármely pontján a paralelogramma oldalán, hogy a vonal, amely a szemben fekvő, párhuzamos oldalán. Jellemzően a magassága a gazdaság a csúcsai a paralelogramma. Mivel a paralelogramma két pár párhuzamos oldala, van egy magassága két különböző hosszúságú.
Magasság \ (BE \) Az elvégzett hosszú oldalai között rövidebb, mint a magassága \ (BF \) között végzett a rövid oldalakon.
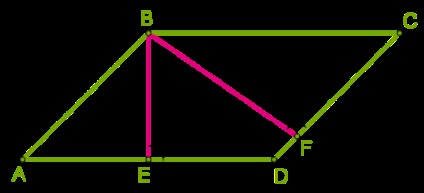
Mivel az oldalán a rombusz azonos, a magassága a rombusz jelentése ugyanaz, mint \ (BE = BF \).
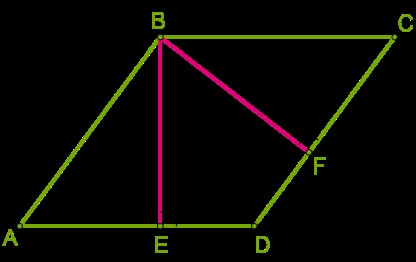
Önkényes területe paralelogramma
A terület egy paralelogramma egyenlő a termék magassága a felek, amelyek birtokában magasságot.
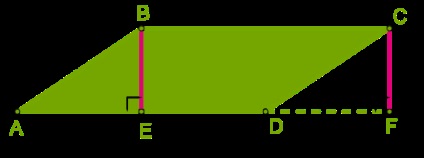
Döntetlen a magassága a két csúcs \ (B \) és \ (C \), hogy az oldalán a \ (AD \).
A téglalap alakú háromszögek \ (ABE \) és \ (DCF \) egyenlő (egyenlő átfogója mindkét átellenes oldalán a paralelogramma és egyenlő lábak közötti távolság a párhuzamos vonalak).
Paralelogramma \ (ABCD \), és a téglalap \ (EBCF \) - egyenlő, mivel ők állnak az egyenlő számokat:
S ABCD = S ABE + S EBCD S EBCF = S EBCD + S DCF
Ennélfogva, a terület a paralelogramma definiáljuk, mint az ugyanolyan, mint egy téglalap terület:
S EBCF = BE ⋅ BC S ABCD = BE ⋅ BC = BE ⋅ AD
Ha jelöljük az oldalsó keresztül \ (a \), a magassága révén \ (h \), akkor:
S n - c = a ⋅ h
Ahhoz, hogy határozza meg a területet egy paralelogramma is használható rövid oldalon és a magasság, párosulnak a rövid oldalon.
Átlói rombusz a kereszteződésekben osztva két, azok merőlegesek, és felosztják a rombusz négy egyenlő derékszögű háromszög.
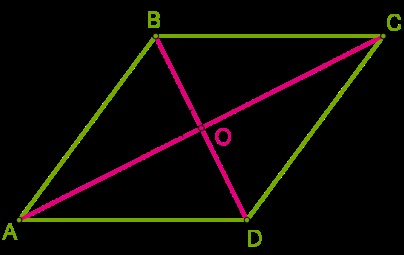
S ABCD = 4 ⋅ S ABO = 4 ⋅ BO ⋅ AO 2 = 2 ⋅ BO ⋅ AO