A térbeli erőrendszer

Home | Rólunk | visszacsatolás

7.1. Statikus invariáns. dinamikus csavar

Korábban azt találtuk, hogy a fő vektor rendszerének erők, a térben tetszőlegesen,

(7.1) nem változik a változás vezetési központ. De a lényeg nem változik, és az új központ működtetjük formula határozza meg

. (7,2), ahol - a fő pontokat hozza a központokat O és. A második tag a jobb oldalon általános képletű (7,2) képviseli a pillanatban a kapott vektort alkalmazzuk, hogy a középső O. viszonylag új vezetési központ.

Skaláris termék mindkét oldalán (7.2) a vektor által:

Mivel a vektor merőleges a vektorba. akkor a skalár szorzat nulla. ezért

. (7.3), azaz skalár szorzata az elsődleges vektora a lényeg nem függ így a központ.

Így, amikor a változó vezetési központ nem módosítja a fő vektor és skalár szorzata a kapott vektor a lényeg. Azt mondják, hogy ezek az értékek állandó tekintetében a választás így a központ.

Az első statikus invariáns az úgynevezett elsődleges vektora. Szűkebb értelemben az első invariáns megérteni a főtér a vektor egység

A második statikus invariáns skalár termék az úgynevezett fő vektor a lényeg:

A második invariáns következik egy egyszerű geometriai következménye. Sőt, tudjuk írni egyenletet (7.3) az alábbiak szerint:

Ezen termékek mindegyike a vetülete a főbb pontok az irányt a kapott vektor. Következésképpen, ha a változó vezetési vetítési központ a fő irányába mutat a kapott vektor nem változik. Megjegyezzük, hogy ha ez a vizsgálat is be lehet venni, mint a meghatározása a második invariáns.

Mivel a vetülete a fő irányába mutat a kapott vektor nem változik, amikor a változó vezetés Center, akkor megállapítható, hogy ahhoz, hogy a központ, amelyben a kapott vektort és pillanatban mentén irányul egy egyenesen, a modul fő pontokat minimális lesz. Ebben az esetben, a kapott pillanatban egyenlő a modul az annak a vetülete az irányt a kapott vektort.

Nyilvánvaló, hogy a kiemelkedés a fő pontok irányába a kapott vektor által meghatározott

vagy figyelembe véve az értékek az első és második invariánsokat

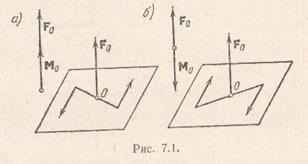
Egy sor erők és pár erőit a pillanatban egy egyenesre erő, az úgynevezett dinamikus csavar vagy dinamit. Mivel a sík merőleges a két intézkedés pont pár, a csavar dinamikus sor erő és a pár ható merőleges síkban erőt. Megkülönböztetni a jobb és bal dinamikus csavarokat. Ábra. ábra dinamikus jobb menetes, alkotják erő. egyenlő fő vektor rendszer és pár erők nyomatéka. egyenlő a fő pont; Ábra. ábra egy bal oldali csavart, egyféle elemek.

A kérdés merülhet fel, hogy mely esetekben ez villamosenergia-rendszer vezethet United? Ez a kérdés a válasz az alábbi tétel:

Ha egy második statikus invariáns nem egyenlő nullával, a villamosenergia-rendszer vezethet dinamó. Ez a kérdés a válasz az alábbi tétel:

Ha a második statikus invariáns nem egyenlő nullával, akkor a rendszer vezethet dinamó.

Legyen tetszőleges pontja a rendszer csökken a teljesítmény egyenlő az elsődleges vektora. és egy pár erőit a pillanatban egyenlő a lényeg. Mivel a hipotézist. Ezután mind a vektor, és a. nem

egyenlő nulla, és ezek nem merőlegesek egymásra. Bővítjük a lényeg két összetevőből áll: az egyik mentén irányul vektort és a másik merőleges a fő vektor fogja irányítani. Ez az a pillanat, erőkomponensként pár található merőleges síkban a vektor. Úgy döntünk, és erő. hogy ezt a

Pár, egyenlő a modulo elsődleges vektor és erőt fejt ki, hogy a központ. A rendszer erők (.) Egyenértékű a nulla, akkor lehet dobni. Mivel az idő - vektor szabad, akkor is át az O pont az a pont. Így az adott rendszer erők látható azon a ponton, hogy erőt és pár erőit a pillanatban. található, egy merőleges síkban, hogy az erő, azaz van egy dinamikus csavart.

Tól (7,6) azt látjuk, hogy a pozitív második megfelel az invariáns dinamikus jobb menetes, és a második negatív változatlan - balra dinamikus csavart.

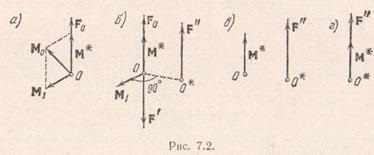
A lényeg nem csak ott, ahol a villamosenergia-rendszer csökken a dinamó. Tény, hogy az erő átvihető a vonal mentén a keresete a pillanatban a két erők vektor ingyenes, ezért a rendszer erői lehet csökkenteni Diname minden pontján az egyenes, amely áthalad a ponton, ahol a hatóirányának erő. Ez a vonal az úgynevezett központi tengelye a villamosenergia-rendszer. Most azt látjuk, a központi tengelye az egyenlet.

Hagyja, - a lényeg a központi tengelye körül. Ezt követően, ezen a ponton a fő vektor és a fő szempont kell egyenesbe egymással. A képlet alapján (7.2) a kapott pillanatra pont felírható

Feltételei kollinearitást a kapott vektor, és az idő a lényeg van írva a következő:

ahol - beállító csavar, amelynek hosszmérete.

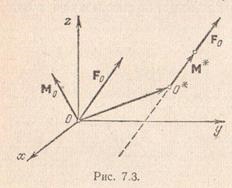
Legyen u - illetve a vetítés a kapott vektor, és a fő pontokat az x tengelyen. y és z; majd

Hagyja, hogy a bármely pont koordinátáit a középső tengely lesz x. y. z. ezért

Behelyettesítve a megfelelő egyenlet (7,7), megkapjuk

Egyenlővé együtthatók az egység vektorok. és. van

Kapcsolódó cikkek

előző ◈ a következő