A normalizált rekord valós számok
Képviselete a valós számok a számítógép határozza meg a tervezési jellemzői számítógépek és szoftverek.
Nprimer, egy 32 bites (4 byte) számos lehetséges ábrázolások következő módszerrel:
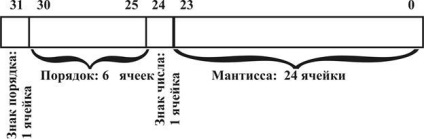
Során számítástechnikai folyamatosan termelt normalizálása közbenső és végső értékek: váltás a mantissza balra és jobbra, míg a változó a sorrendben. Amikor eltolódásokat elveszett számjeggyel a mantissza, hogy van, hogy növelje a számítási hiba.
Mintegy túlfolyás változók valós tranzakciók:
Mantissza ne érjen. normalizálódnak.
Az eljárás lehet túlfolyó.
Például egy kör ábrázolása egy valós szám, a fenti van:
Precíziós megmunkálás valós számok eh forma függ az ötlet:
Pontosság - száma számjeggyel a mantissza
Javítása számítások pontosságának igényel nagy számítógépes erőforrásokat, növeli a számítási idő.
Az egyik szempont az optimalizálása algoritmusok és programok azok végrehajtására: a kompromisszum a pontosság és a számítási költséggel számítógépes erőforrások (idő).
Minél több bit jut a felvétel a mantissza, annál nagyobb a pontosság a számok.
Minél több bit veszi a rend, a minél szélesebb számokat a gép nulla a legnagyobb számban.
Valós méret m - bit mantissza lehetővé teszi, hogy elképzelni pontosan m - bites egész. azaz bármilyen bináris egész álló nem több, mint m-bit, torzítás nélkül lehet képviselve valós formátumban (rácspontok).
Egy példáját szemléltető kísérlet №1.
Tekintsük a kifejezést: R = N * 1 / N # 9472; 1.
1. A matematika, R = 0 minden N.
2. Ha a programozás. Lássuk, mi fog történni, ha a program egy kifejezés:
Ha megad N - tetszőleges valós típusú,
megkapjuk R ≠ 0, (R≈10 -11, ha R már le, mint valódi).
Ha meghatározott N = 2 m. ahol m<=8, то получим R=0 – точный результат.
Egy példáját szemléltető-kísérlet №2.
1. A matematika: 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1 = 1
2. Ha a programozás:
R: = 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1; megkapjuk R≈1
Összegezve tehát nem vevő egység.