A módszer a Gauss-Jordan
„Ha azt szeretnénk, hogy megtanulják, hogyan kell úszni,
ne habozzon, írja be a víz,
de ha azt szeretnénk, hogy megtanulják, hogyan kell megoldani a problémákat.
majd megoldja őket. "
D. Polya (1887-1985 g)
(Matematikus. Ő tett egy nagy hozzájárulás
a népszerűsítése a matematika.
Írt több könyvet
hogyan lehet megoldani a problémákat, és
megtanulják, hogyan kell megoldani a problémákat.)
Algoritmus Gauss-Jordan megoldására rendszerek lineáris egyenletek
2) válassza ki a fogadó elem (minden nem nulla elemet) minden sorban és minden oszlopban az utolsó kivételével. (Sor és oszlop, amelyben az úgynevezett vezető).
3) futtatása a Jordán deléció vezető a kiválasztott elemet. Megjegyzés: a vezető és valamennyi vonal korábban megjelölt.
4) Ha legalább egy sort formájában (0 0 ... 0. b), b ≠ 0, akkor a rendszer nem megoldások. Válasz. A rendszer nem felel.
5) Ha az összes nulla mátrix sorai a címkével, majd írjuk le a rendszert, és megtalálja az általános megoldást. Válasz. Az általános megoldás.
6) válassza ki a vezető eleme minden címkézetlen sorban és minden oszlopban az utolsó kivételével. Folytassa a 3. lépéssel.
Fuss a Jordán kivétel vezető elementomaij a következőket jelenti:
1) osztja a vezető sorban a vezető elem;
2) töltse ki a szabad helyet a vezető nullákat oszlop;
3) a megmaradó mátrix elemek megszámoltuk a képlet, az úgynevezett „a szabály a téglalap.”
Képzeljük azt általában vázlatosan. Hajtőelemmei osztja keretben. A nyilak mutatják az elemeket, amelyeket szorozni a számlálóban. Ezek az elemek vannak elrendezve, az átlók a téglalap által képzett vezető elem Aij. újraszámítja elem AKL és elemeket, amelyek a kereszteződésekben a vezető sor és oszlop l. vezető az oszlop és sor k.
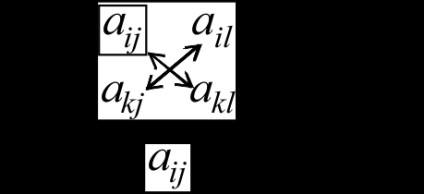
Notes.
1. A számlálóban mindig a termék egy vezető elem (függetlenül attól, hogy mi az első a téglalap érdemes hajtóelem) levonjuk terméket az elemek, amelyek a kereszteződésekben a pivot sor és oszlop l. vezető az oszlop és sor k.
2. Ha a hajtáslánc a nulla elem, az oszlopot, amelyben található a Jordán kizárás nem változik.
3. Ha a vezető oszlop a nulla elemet, a vonal, ahol ez található a Jordán kizárás nem változik.
Tekintsük a példát megoldani rendszerek Jordan-Gauss.

Mi írja le a kiegészített mátrix rendszer

Kiválasztása hajtőelemmei (meghajtó elem osztja frame):

Végezze el a Jordan kivételével a vezető elem a13 = 1.
1) osztott a vezető vonal 1;
2) töltse ki a szabad helyet a harmadik oszlopban a nullák;
3) a vezető oszlopban a második sorban a nulla elemet (A23 = 0), így a második sorban újraírás változatlan (Megjegyzés 3);
4) A fennmaradó mátrix elemeinek (nevezetesen, a fennmaradó négy sor a harmadik elem) számítani az „szabály a téglalap.”
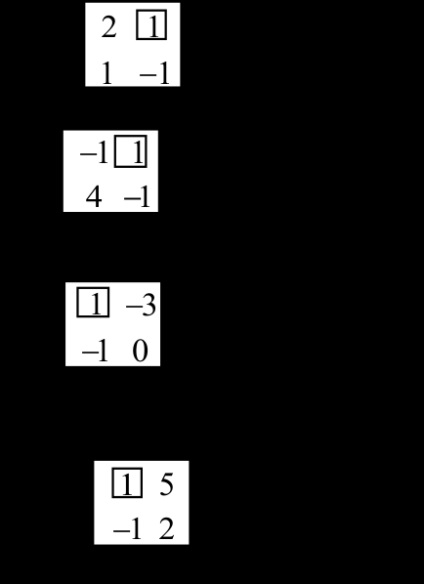
A kapott mátrix lesz az első sorban ellenőrzés:

Most ez a mátrix válasszuk ólom (minden nem nulla) eleme minden címkézetlen sorban és minden oszlopban az utolsó kivételével, például a21 = 1.

Végezze el a Jordan kivételével a vezető elem A21 = 1:
1) osztott a vezető vonal 1;
2) töltse ki a szabad terület az első oszlopban a nullák;
3) a harmadik oszlopban meghajtó vonal a nulla elemet (A23 = 0), és így a harmadik oszlop átírni változatlan (2. megjegyzés);
4) újraszámítja a maradék a mátrix elemei „szabály téglalap”.
Tick ólom (második) sor és jelölt vonal korábban.
Az eredmény egy mátrix:

A végső mátrixa a harmadik sorban minden elem, kivéve az elemek az utolsó oszlopban nulla. Következésképpen, a rendszer inkonzisztens (n. 4. algoritmus Gauss-Jordan megoldási módja rendszerek lineáris egyenletek).
VÁLASZ: A rendszer nem felel.
