A minimális sebesség a test mozgás dobott szögben
Állapota a problémát:
A minimális sebessége a test mozgás dobott szögben a vízszintes 5 m / s, és legfeljebb 10 m / s. Hogy meghatározza a szöget, amely a test öntött.
№1.6.4 feladata a „Collection feladatok előkészítése a felvételi vizsgák a fizika UGNTU”
Megoldás:
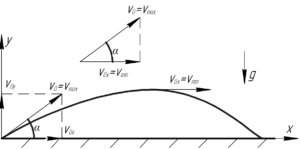
Megmagyarázni a döntést fogom használni a következő tény, hogy bármikor a sebességet a test bontható komponensek, akkor a legtöbb lebomló ráta megtalálható a Pitagorasz-tétel:
Most ne feledjük, hogy a test mozgása dobott szögben a vízszintes, vízszintes összetevője a sebesség \ (v_x \) nem változik, hiszen a mozgás mentén \ (x \) egyenletes (E tengely mentén nem kell alkalmazni erő), és a függőleges komponense sebesség \ (v_y \) változnak a maximális idején dobott nullára a legmagasabb ponton, és vissza. És ugyanaz lesz, mint amikor dobott (kivéve persze, hogy a Föld felszínén olyan sima, mint mi az ábrán) idején a leesik a földre, a két komponens (és így a sebesség is).
Kiderült, hogy ha az arány határozza meg a fenti képlet, a legkisebb értéket veszi a legmagasabb ponton, amikor a \ (v_y = 0 \) m / s, a legnagyobb - a dobás pont és esik vissza a felszínre.
Nézzük a rajzot, akkor látható, hogy a szög a vektorok ezeknek megfelelő sebesség és a szög a test öntött. Erre a derékszögű háromszög koszinusz \ (\ alpha \) határozzuk meg a következő képlet.
Mi helyettesíti az ismert adatok és így a válasz:
\ [\ Alpha = \ arccos \ frac> = 60 ^ \ circ \]
Válasz: 60 ° C.
Ha tetszik a probléma és annak megoldása, akkor ossza meg ismerőseivel Ezekkel a gombokkal.