A megoldás a közlekedési probléma az Excel, mslegko
A szállítási probléma - matematikai lineáris programozási feladat egy speciális formája a keresést az optimális elosztása hasonló tárgyakat az akkumulátortól a vevők, hogy minimalizálja a mozgó költségeket. A könnyebb megértés, tekinthető a probléma az optimális terv rakomány kiindulási pont, hogy pont a fogyasztás, minimális forgalom.
Ha a teljes mennyiség javaslatok (az áru rendelkezésre a kiindulási pontja) nem egyenlő a teljes mennyiség kereslet az áruk (termékek), a kért terméket a fogyasztás, a közlekedési probléma az úgynevezett kiegyensúlyozatlan (nyitott).
Ha a teljes ellátási térfogata megegyezik a kötet a kereslet, a közlekedési probléma a zárt típusú, vagy úgynevezett zárt.
A szállítási probléma (klasszikus) - a probléma optimális szállítási tervet homogén termék homogén pontok, egységes fogyasztási pontok homogén eszközök (előre meghatározott mennyiséggel) statikus és az egyenesre megközelítés (ezek a fő feltételek a probléma).
Az ilyen problémák megoldására Excel egy speciális eszköz „A keresés megoldás”. Felépítmény „Search megoldás” Microsoft Excel lehetővé teszi, hogy közvetlenül megtalálja az optimális megoldást a közlekedési problémát.
Ahhoz, hogy az add-in „Megoldások” ha „Adatok” fülön a tétel nem megy Fájl - Beállítások. „Kiegészítők” a bal oldali menüben válasszuk. A fő eseménye a „keresd a megoldást.” Akkor alul, kattintson a „Go”. válassza ki a „Search megoldás” a megnyíló ablakban, és kattintson az „OK” gombot. Az „Adatok” fülön az adott tétel az azonos nevet.
Az általános állapota a közlekedési problémát:
Keresse m * n nem negatív egész xij - a forgalom az i-edik szolgáltató a j-edik felhasználó, minimalizálva a szállítási költségeket a szállítás homogén áru szállítók kapacitása (tartalék), A1, A2, ... Am a fogyasztóknak kell B1, B2, ... Bn. ha tudjuk, hogy a mátrix Sij költségeket - a költségek a rakományt szállító egységek az i-edik szolgáltató a j-edik felhasználó.
A matematikai megfogalmazása a probléma:
^&space;X_&space;=&space;A „/> i = 1,2 ... .m
Tehát szükség van a közlekedés a feladat az volt, zárt -summarnaya áramszolgáltatók egyenlőnek kell lennie a teljes a fogyasztók igényeinek.
^&space;X_&space;=&space;Bj „/> j = 1,2, ... .N
Ha egy nyílt kihívás az egyensúly teljes tartalék és szüksége bemenet vagy egy bábu, amelynek a tartalékok a többlet teljes igényeit a teljes tartalék, vagy egy fiktív fogyasztói igények megegyeznek az meghaladja a teljes tartalék a teljes kereslet. Így a költség mátrix sorban vagy oszlopban van kiegészítve nullákkal.
Egy példa a probléma és annak megoldása MS Excel.
Mivel 5 termelők A1, A2. A3, A4. A5. teljesítmény (tartalékok), amelyek rendre egyenlő (egyenlő): 20, 45, 25, 30,20.
És a négy fogyasztó B1. B2. B3. B4. követelmény, amelyet a termék, illetve 45, 50, 20, 25.
Szintén ismert mátrix Sij költség - a költségek a rakományt szállító egységek az i-edik szolgáltató a j-edik felhasználó.
Lehetőség van, hogy bemutassa a táblázat:
A cellatartomány A2: A6 be a készletek beszállítók - Ai:
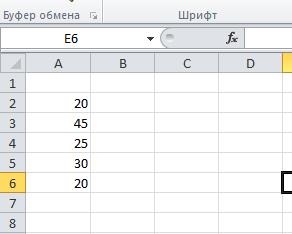
A cellatartomány B1: E1 adja meg a számot a kívánt rakomány Bj th fogyasztó:
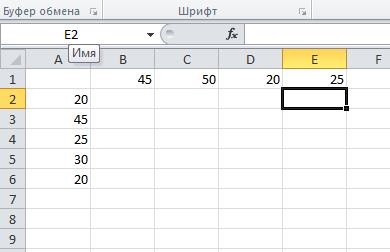
A további kényelem, jelöljük ki a cellát, különböző színekben és állítsa be a zsír határ:
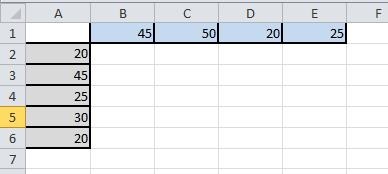
A cellatartomány B2: E6, írja be a mátrix Cij egység rakomány szállítási költségek az i-edik szolgáltató a j-edik a fogyasztó számára:
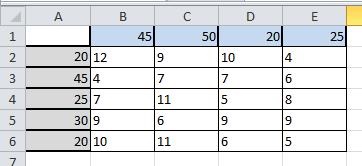
A sejt-H1 írja be a képletet: SUMMAPROIZV (B2: E6; B9: E13)
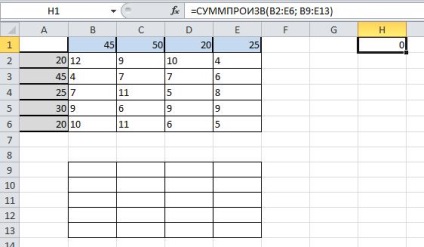
A sejt A9 típusú SUM (B9: F9) formula, és húzza át az A13 (lásd, hogyan nyúlik a képlet itt -> Tyc.):
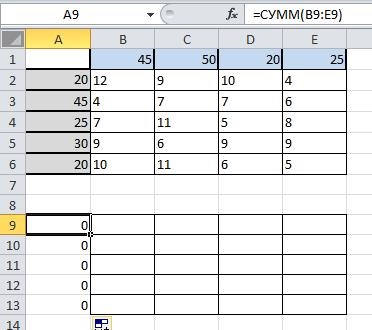
A sejttípus a képletben B8 SUM (B9: B13), majd másolja a tartományban B8 E8:
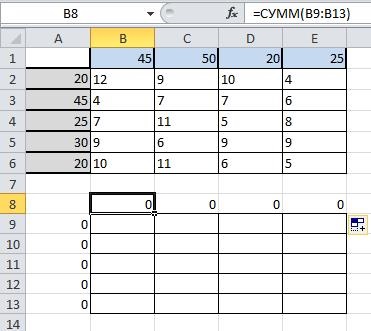
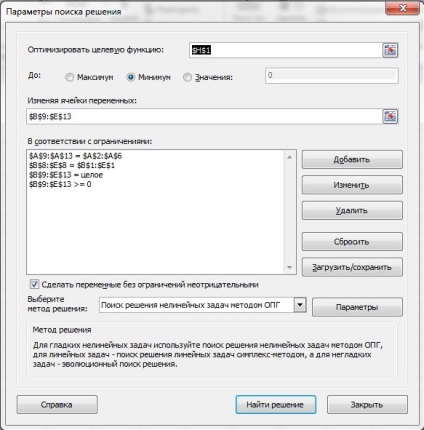
A probléma megoldása érdekében a lap bár, válassza ki a fület „Data”, majd a „Keresés megoldás”:
Töltse ki az ablakba szerint egy képet, és nyomja meg a Find a megoldást:
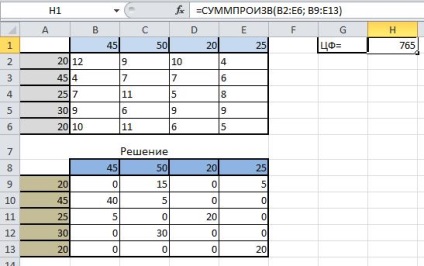
A tartomány B9: E13 kap az eredménye megoldására közlekedési probléma (azaz az értéket a cella mennyiségének felel meg a szállított rakomány által az i-edik szolgáltató a j-edik ügyfél).
A tartomány A9: A13 árumennyiség szállítják a szállítók.
A tartomány B8: E8 fogyasztók számát kell szállítani szerint keresett megoldást.
A H1 a cella értékét a célfüggvény a megoldást találtuk (a lehető legalacsonyabb). Ezt az értéket úgy kapjuk meg, a szállítási költségek a i-edik a kapcsolatot a j-edik felhasználó a rakomány mennyiségétől egységek, amelyeket el kell szállítani közöttük.
Mi megszervezzük az eredményt, és így a következő:
Töltse olyan fájlt, amelyet a folyamat halad a leckét akkor itt -> Transportation_problem