A központjai közötti távolság a sugarak körök 1 és 9 17
A központjai közötti távolság a sugarak körök 1 és 9 egyenlő 17. Ezek a körök és azok közös belső érintője tekintetében a harmadik kört.
a) Bizonyítsuk be, hogy a vonal a érintési pont egybeesik az érintési pont az egyik első két kört.
b) Mekkora a sugara a harmadik kört.
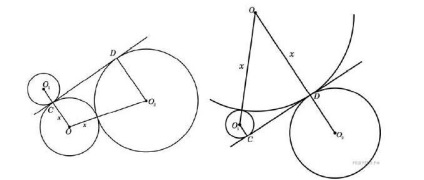
a) Legyen x a sugara a szükséges kör O középpontjában. CD belső érintője körök adatait O1 és O2 - a központ. Megjegyezzük, hogy a vonal CD - közös külső érintője köröket központok O és O 2 (ábra ..), Or köröket központok O és az O1 (ábra ..). Ezen a ponton is érinti az egyenes egybeesik az érintési pont az első két kör, mivel a tangens átjusson egy közös pont (érintési pont) körök.
b) meghatározza a sugár a harmadik kör első bizonyítéka a következő állítás. Ha egy központjai közötti távolság a körök sugarai R és r, a⩾r + R, közös külső érintője az érintő a köröket A és B pontok, a belső a C és D pontok, majd
AB = sqrt (a ^ 2- (R-R) ^ 2), CD = sqrt (a ^ 2- (R + R) ^ 2).
Valóban, tegyük fel, hogy a központok O1 és O2 körök sugarai R és R, illetve (lásd. 2. ábra). A pontok O1 és O2 O1Q csepp egy merőleges egyenes és O2V O2F közvetlen O1S. A derékszögű háromszög és O1QO2 O1FO2 azt találjuk, hogy
O1Q = sqrt (O1O2 ^ 2-QO2 ^ 2) = sqrt (a ^ 2- (Rr) ^ 2), O2F = sqrt (O1O2 ^ 2-FO1 ^ 2) -sqrt (a ^ 2- (R + R) ^ 2).
Következésképpen, CD = O2F = sqrt (a ^ 2- (R + R) ^ 2).
A fenti CD = sqrt (17 ^ 2 (1 + 9) ^ 2) = sqrt ((17-10) (17 + 10)) = sqrt (7 * 27) = 3sqrt (21)
Az első esetben a CD-közös külső érintője egy O középpontú kör és O2, így CD = sqrt ((x + 9) = 2- (9-x) ^ 2) = 6sqrt (x)
6sqrt (x) = 3sqrt (21)
2sqrt (x) = sqrt (21)
4 = 21
X = 5,25
A második esetben a CD-közös külső érintő a köröket a központok O és O1, így CD = sqrt ((x + 2) = 2- (2-x) ^ 2) = 2sqrt (x)
2sqrt (x) = 3sqrt (21)
4x = 189
X = 47,25
Levél + regisztrációs egyetlen kattintással