A koncepció az integrál egyenlet
Nevükön integrálegyenletek járó ismeretlen függvény alapján az integrál jel. Ez a meghatározás nem túl jó. A cím alatt „integrálegyenletek” ismert dolog, egy kicsit hasonlít egymásra. Általában ne próbálja, hogy egy általános meghatározás szerves egyenletek, és kizárólag erre a listára a legfontosabb osztályok szerves egyenletek.
Az egyik legfontosabb és jól tanulmányozott osztálya lineáris integrálegyenletek az egyenlet Fredholm II-es típusú. Az úgynevezett egyenlet a következő formában:
(Ezzel szemben a egyenletek formájában
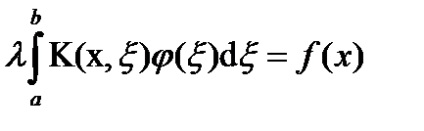
Ha f (x) = 0, az integrál egyenlet homogén; egyébként - egységes.
Funkciója két valós számot nevezzük a kernel az egyenlet; paraméter # 955; - kompiexértékű. A mag határozza meg a box: a≤x, # 958; ≤b.
A kernel a (1) egyenlet azt sugallja, hogy
A szabad kifejezés f (x) Az (1) egyenlet kielégíti
Egy hasonló egyenlőtlenség feltételezzük, hogy tartsa az ismeretlen függvény # 966; (x).
Abban az esetben, (3) az f (x) nevezik integrálható az (a, b). A kernel az integrál egyenlet állítólag tér-integrálható a a≤x téren # 958; ≤b.
Fredholm vizsgálták az esetet, amikor # 966; (x), f (x) - a folytonos [a, b], és a
- folyamatosan a főtéren a≤x, # 958; ≤b. Nyilvánvaló, hogy ebben az esetben is tart (3).
A szerves egyenlete formájában (1) szerves egyenlet egy gyenge funkciót, ha a kernel az egyenlet
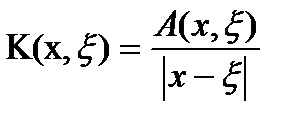
ahol - a folyamatos funkció a≤x, # 958; ≤b. Ebben az esetben az egyenlet is nevezik különleges vagy egyedi.
Általában, az integrál egyenlet nevezzük szinguláris, ha vagy a vagy b végtelen; vagy nucleus végtelenné válik egy vagy több pontot az intervallum.
A speciális esete az (1) egyenlet egy egyenlet a következő formában:
Ez az egyenlet az úgynevezett egyenlet Volterra típusú diabétesz.
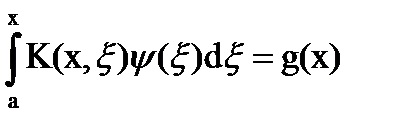
úgynevezett Volterra típusú egyenlet (ezek nem veszik figyelembe).
A tulajdonságait a integrál egyenlet, ez határozza meg a tulajdonságait a megoldások sejtmagba.
Erre a kernel tárgyalja:
1) ültették mag (5)
2) kétmagos (6)
Ha csak valós értékeket, akkor.
Ez a kernel neve:
Hermitian ha igen,
kritikus, ha tartja (2) és az integrálási ≠ 0,
folyamatos, átlagban, ha
,
degenerált (vagy elkülöníthető), ha
.
Lineáris szerves szereplő úgynevezett transzformációs (mapping)
(1) egyenlet felírható: (7)
Volterra integrál egyenlet II típusú csökken a Fredholm egyenletet (0, ∞), ha belépsz egy új kernel
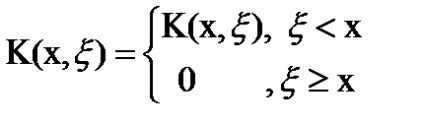
Megoldás az integrál egyenlet függvénye # 966; (x), amely, ha szubsztituált egyenletbe felhívja be identitás relatív.
Példa. Ellenőrizze, hogy a megoldás az integrál egyenlet
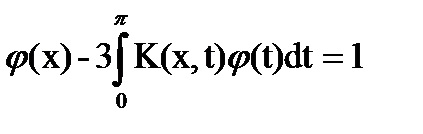
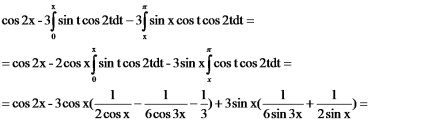
Integrálódni részből áll:
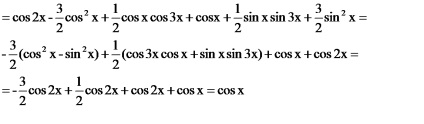
A: A funkció a megoldást az integrál egyenlet.
gyakorlatok:
1.Pokazat hogy ezek a funkciók megoldásaik a szerves egyenletek.