№3-mechanika előadás
Téma: „Belső erők a keresztmetszet a rúd”
1. A támogatások és támogatási reakciókat és azok meghatározása
2. A keresztirányú erő és hajlítónyomaték
3.Vzaimosvyaz között hajlítónyomaték, nyíróerő és intenzitása megoszló terhelés
1.Opory és támogatás reakciókat és azok meghatározása
Kiszámításakor konstrukciók elemek javarészt tapasztalt hajlítás. A rudak futó túlnyomórészt hajlítási nevű gerendák. Sugározni lehet betölteni, és azt továbbítja a bázis, meg kell vele kapcsolatban ellátott kötvényeket. A gyakorlatban használható többféle hivatkozásokat, vagy ahogy mondják, többféle támogat.
Három fő típusú támogatást tartalmaz:
a) csukló-mozgatható hordozótag:
b) közös rögzített támogatás:
c) rögzítési.
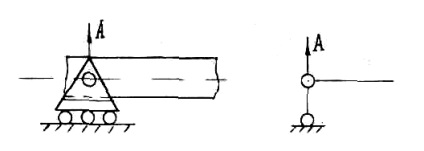
Ábra. Az 1. ábra egy csuklósan mozgatható hordozóra, így támogatás lehetővé teszi a fény szabadon elforgatható és mozog a vízszintes irányban. Ezért, a reakció a támogató egyike lesz függőleges erő. Symbol támogatási jobbra látható.
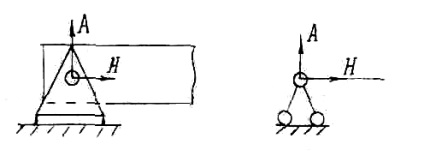
Ábra. A 2. ábra a csukló-rögzített csapágy. Ez a támogatás lehetővé teszi a fény szabadon forogni, de nem tudja mozgatni. Ezért előfordulhat, hogy két reakció - a függőleges és vízszintes erőket. Ők lehet hajtani, és kap egy rezultatiruyuschuyu erő, de meg kell tudni, hogy a szög a Rostral fog küldeni. Sokkal kényelmesebb használni a függőleges és vízszintes komponensei a reakciót.
Ábra. A 3. ábra a rögzítési. Ez nem teszi lehetővé a sugárzó forgatni vagy mozgatni. Ezért előfordulhat, hogy három támogató reakciók: Jelenleg a függőleges és vízszintes erőket. Ha a fény nem érintik a végén, ez a része az úgynevezett konzolt.
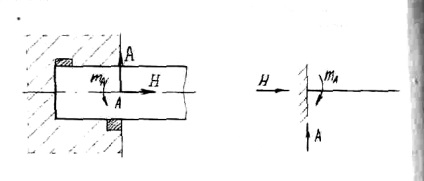
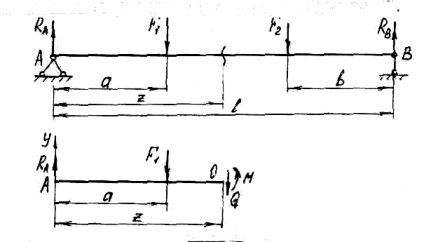
Határozza hordozók a reakció a gerenda (lásd. Ábra. 4).
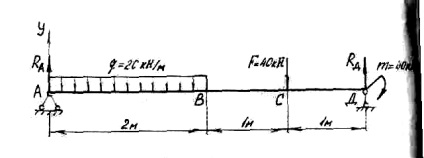
A hordozót és a vízszintes reakció nulla, mert a megoszló terhelés q és koncentrált F erő van függőleges irányban. támogatás reakciók
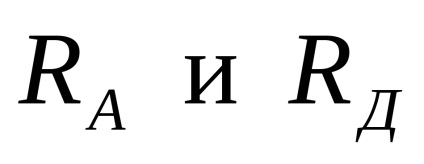
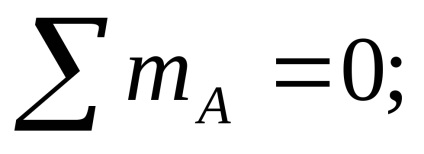
ahol
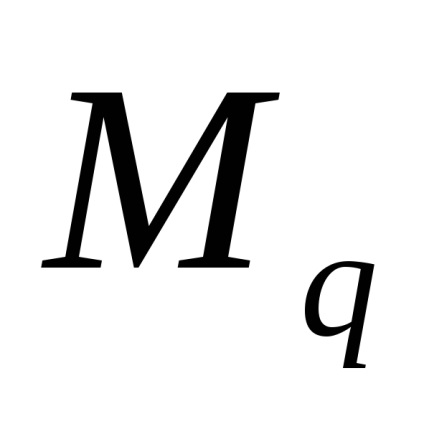
A terméket a q által a távolság, amelyen azt alkalmazzuk, az egyensúlyi állapotban a rendszer megegyezik a koncentrált erő a közepén a szegmens. Ezért az idő
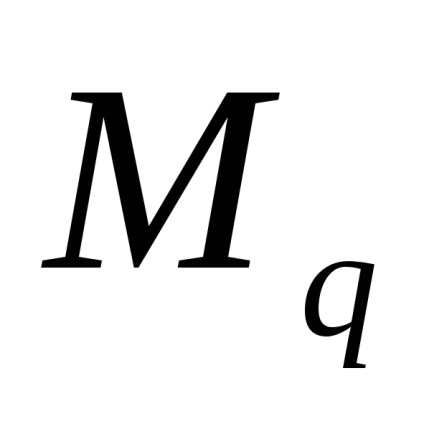
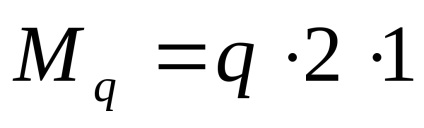
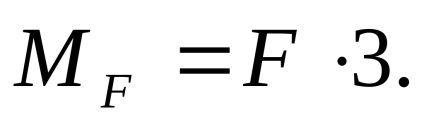
Külső pillanat m, a váll nem szorozni, mint egy pár erők, vagyis a két egyenlő nagyságú, ellentétes irányú erők, amelyek egységes vállát.
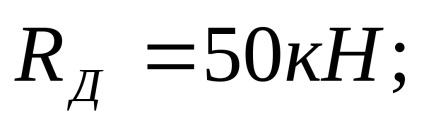
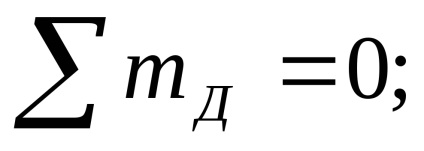
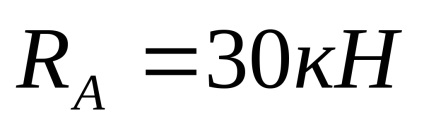
Tesztelés: az összeg minden erő a függőleges Y tengelyen kell nullával egyenlő:
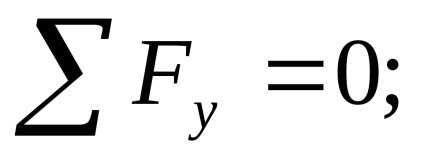
.
M nyomatékot a feltétele statikus egyensúlyi
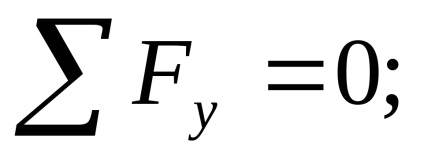
A reakciókat megfelelően definiálva.
2. A keresztirányú erő és hajlítónyomaték
Hagyja, hogy a gerenda erők jogszabály
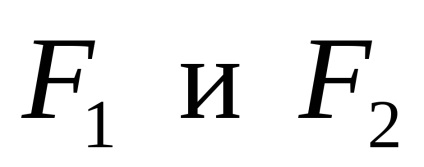
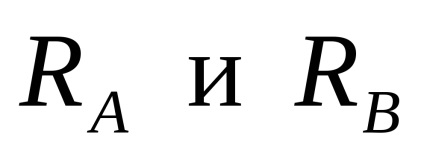
Mivel minden ható külső erők függőlegesen, vízszintes összetevője a padló reakció Egy nem. A sugár nem fog zsugorodni, vagy nyúlik, azaz a hosszanti erő a keresztmetszete nulla. Lehet, hogy egy példát, amikor az erők
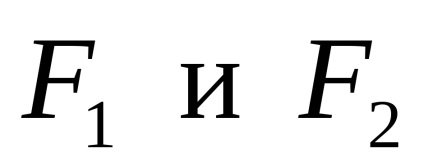
Mivel a külső erők
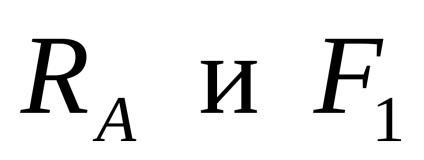
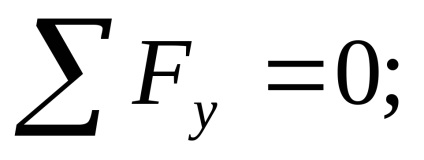

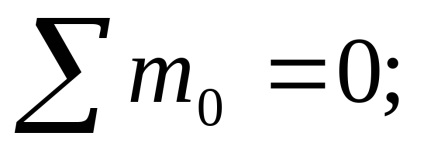
.
Következtetés: A nyíróerő a részben numerikusan ravnaalgebraicheskoy összege minden külső erők és hajlítónyomatékot momentsumme összes számított, hivatkozással a szekcionált iprilozhennyh tekinthető része a nyaláb.
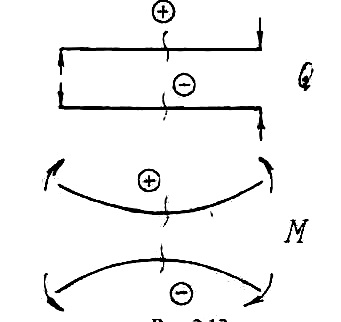
A keresztirányú erők és hajlítónyomatékokat teszi kötelező szabályai jelek (lásd. Ábra. 6.).
Ha az erő próbálva a részének tekintik a fény az óramutató járásával megegyező irányba, akkor ez egy pozitív oldalirányú erő, és éppen ellenkezőleg, ha a cselekmények az óramutató járásával ellentétes oldalirányú erő negatív. Ábra. 5 szilárdság

Ha a külső erő vagy külső nyomaték gerenda lefelé hajlik convexity, a felmerülő hajlítónyomaték pozitív, és fordítva, a negatív convexity felfelé .
3. A kapcsolat a hajlítónyomaték,
keresztirányú erő és intenzitása elosztott terhelés
Legyen a konzolos tartó (lásd. Ábra. 7) működik elosztott terhelés, amely hossza mentén változó a gerenda. A z távolságra a bal végén a take infinitezimális szegmens dz.
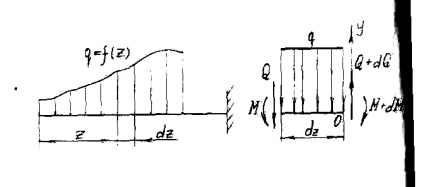
Ezután a megoszlása a terhelés akkor tekinthető állandónak. A bal oldalon a szegmens megfontolás alatt vannak a belső erők Q és M a jobb figyelembe véve a növekmény belső erők Q + DQ és M + dM.
statikus egyensúlyi egyenletet, hogy létrehozzák a gerenda hossza:
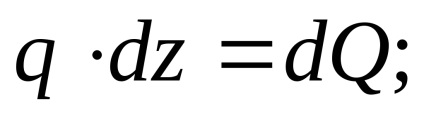
A harmadik ciklus lehet hanyagolni, mint egy végtelenül magasabb rendű, azaz.:
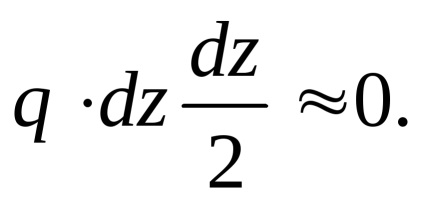
A transzformációk után kapjuk:
azaz az első származékot a hajlítónyomaték az abszcisszán (a hossza a fény) a nyíróerő.
Ha a fenti (1), hogy helyettesítse a Q érték a (2) képletű, kapjuk:
azaz A második deriváltja a hajlítónyomaték a megoszló terhelés intenzitását.